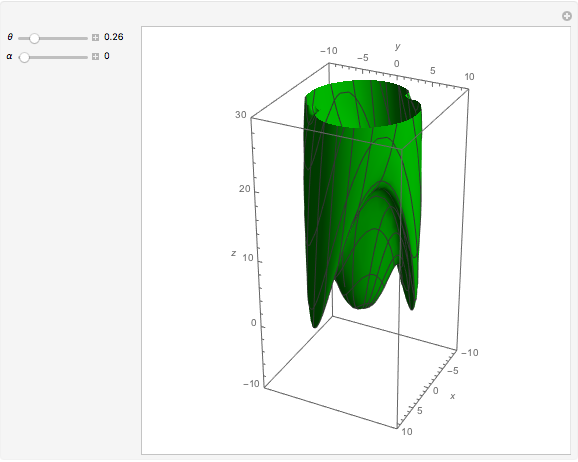
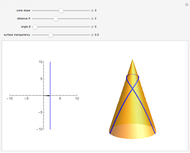
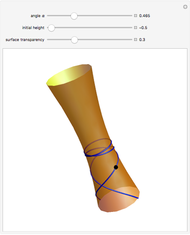
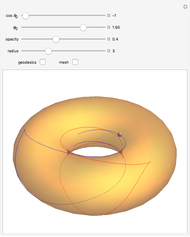
Geodesic Cone in Nil-Geometry

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
W. Heisenberg's real matrix group provides a noncommutative translation group of an affine three-space. The Nil-geometry, which is one of the eight Thurston three-geometries, can be derived from this group. E. Molnár proved that the homogeneous three-spaces have a unified interpretation in the projective three-sphere 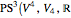 ). In this Demonstration a geodesic line rotated around the
). In this Demonstration a geodesic line rotated around the  axis, (a "geodesic cone") is visualized.
axis, (a "geodesic cone") is visualized.
Contributed by: Benedek Schultz and János Pallagi (July 2009)
Suggested by: Jenő Szirmai
Open content licensed under CC BY-NC-SA
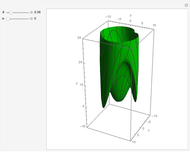
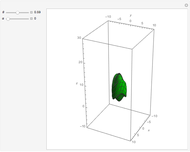
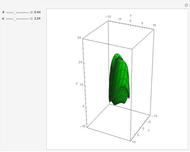
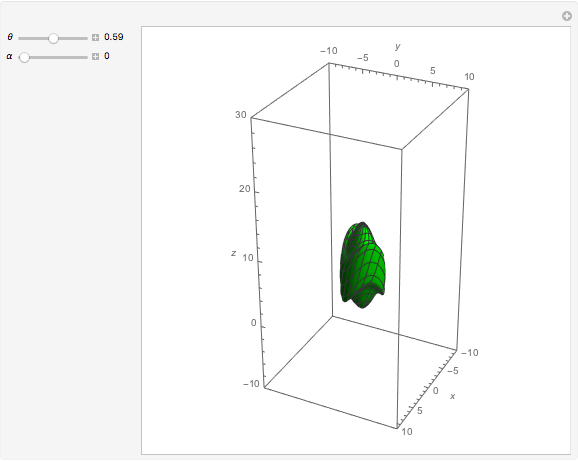
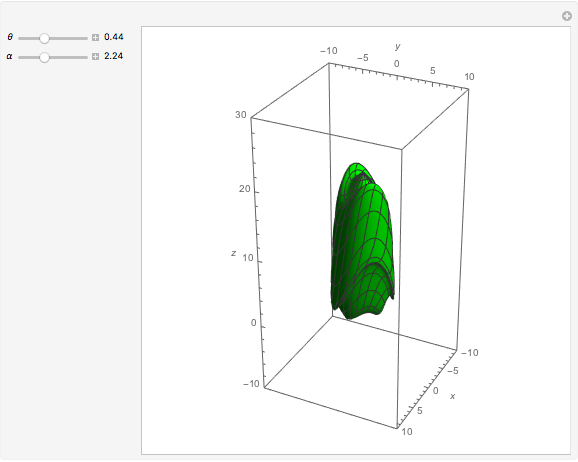
Snapshots
Details
You get a "geodesic cone" by rotating a geodesic curve around the  axis. The geodesic curves of the Nil-geometry are generally defined as having locally minimal arc length between any two (near enough) points. The system of equations of a parametrized geodesic curve is (where
axis. The geodesic curves of the Nil-geometry are generally defined as having locally minimal arc length between any two (near enough) points. The system of equations of a parametrized geodesic curve is (where 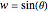 ,
, 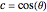 ):
):
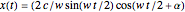 ,
,
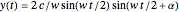 ,
,
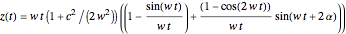 ,
,
if  , and
, and
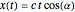 ,
,
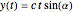 ,
,
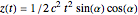 ,
,
if 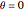 .
.
Here  and
and  are the parameters of a geodesic curve (
are the parameters of a geodesic curve (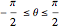 ,
, 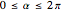 ); in this Demonstration you can adjust these values.
); in this Demonstration you can adjust these values.
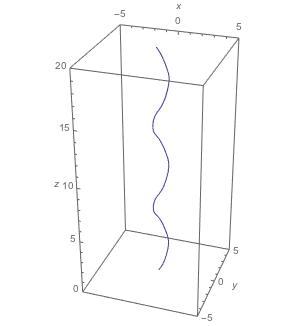
The following is an example of a geodesic curve with parameters  ,
,  :
:
A point 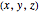 rotated through
rotated through 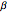 has the following coordinates: (
has the following coordinates: ( ,
, 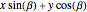 ,
, 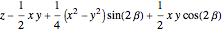 ).
).
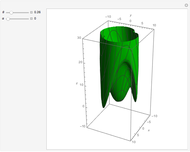
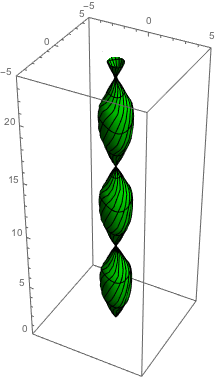
As you can see, a geodesic curve returns periodically to the  axis. We get the "geodesic cone" by rotating the part of the geodesic curve between the origin and the first return to the
axis. We get the "geodesic cone" by rotating the part of the geodesic curve between the origin and the first return to the  axis around the
axis around the  axis.
axis.
If we rotated the whole curve, then it would look like this (with  ,
,  ):
):
In this Demonstration you can adjust the  and
and  parameters, and according to this, the
parameters, and according to this, the  parameter (the arc length parameter) has a value
parameter (the arc length parameter) has a value 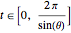 .
.
Reference:
J. Szirmai, "The Densest Geodesic Ball Packing by a Type of Nil Lattices," Beiträge zur Algebra und Geometrie (Contributions to Algebra and Geometry), 48(2), 2007 pp. 383–397.
Permanent Citation