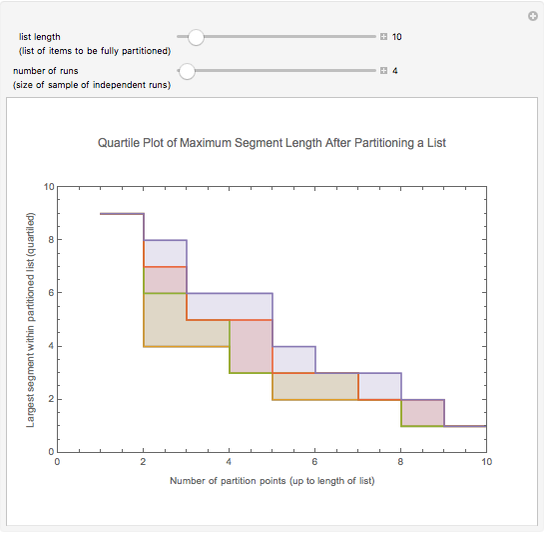
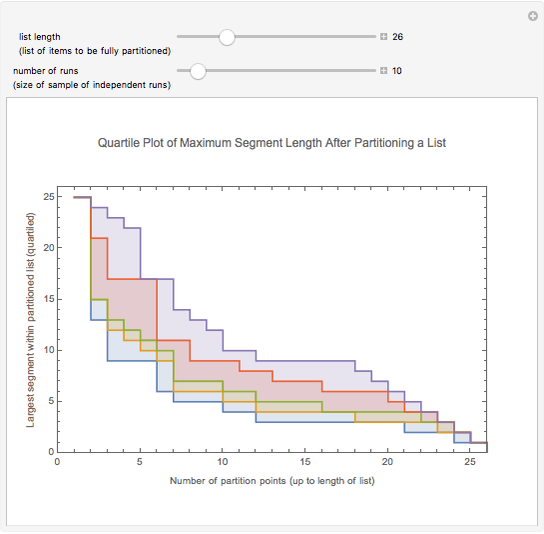
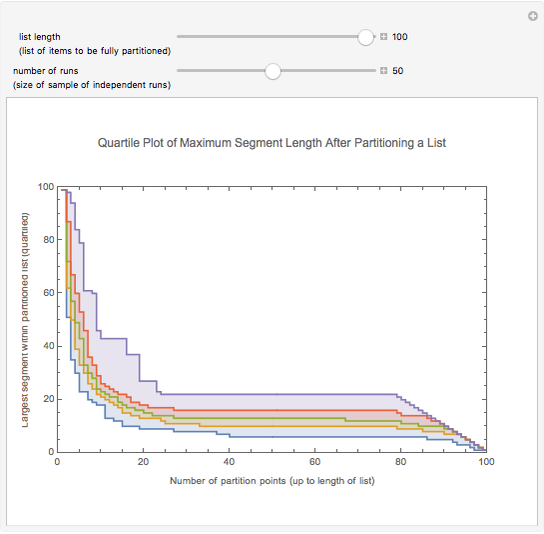
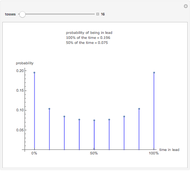
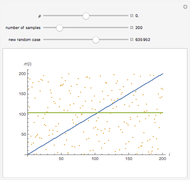
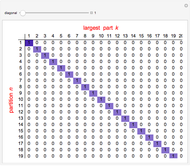
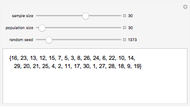
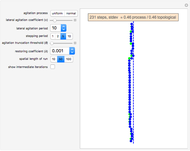
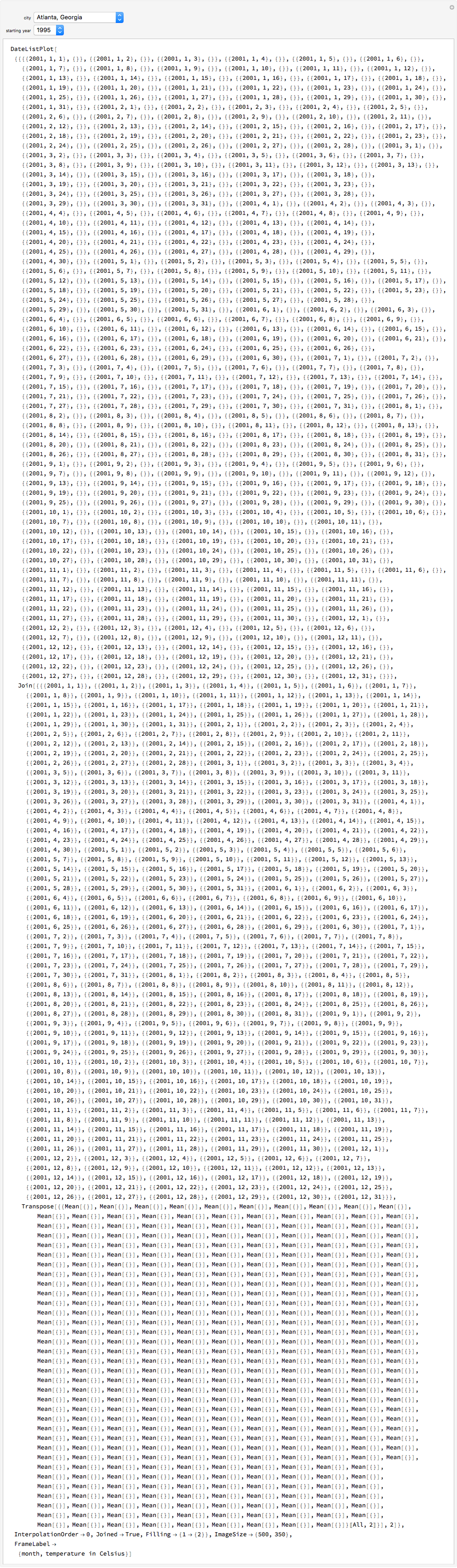
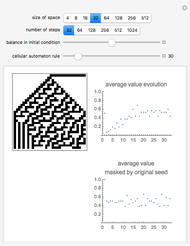
The list of integers from 1 to is successively partitioned at random points until the list is totally partitioned. At each iteration the maximum segment lengths of the lists are analyzed statistically over the sample of runs and the quartiles are plotted. This sequence is plotted from right to left on the abscissa. Quartiles (plotted on the ordinate) are marked in different colors. For longer runs the plot exhibits phases of behavior. Over the first few partitions the maximum segment lengths drop quickly. Then there is a stable region where the maximums drop slowly. Near the end the maximum steps down to 1 as the process is constrained to terminate at a full partition.