Rational Linear Combinations of Pure Geodetic Angles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
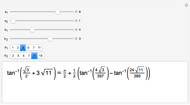
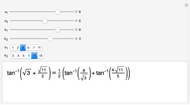
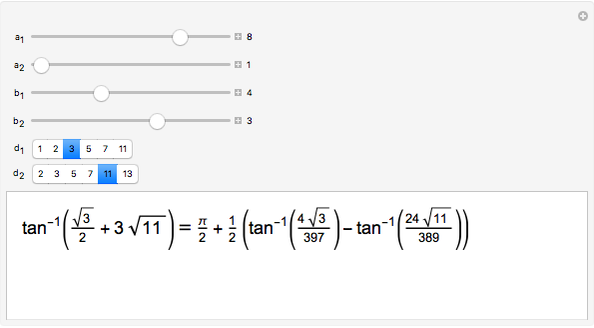
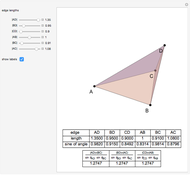
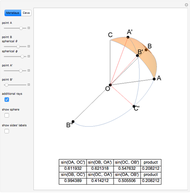
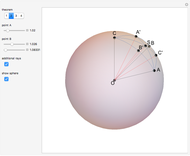
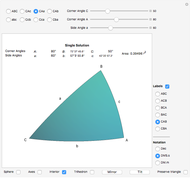
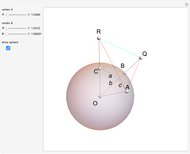
A "pure geodetic" angle is an angle with any of its six squared trigonometric functions rational (or infinite). This Demonstration shows how an angle whose tangent is of the form 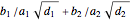 can be expressed as a rational linear combination of pure geodetic angles and an integral multiple of
can be expressed as a rational linear combination of pure geodetic angles and an integral multiple of 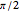 , that is, it finds rational
, that is, it finds rational 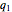 and
and 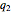 such that
such that 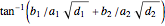 is a sum of
is a sum of 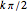 , where
, where 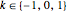 and a rational linear combination of
and a rational linear combination of 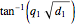 and
and 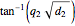 .
.
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] J. H. Conway, C. Radin, and L. Sadun, "On Angles Whose Squared Trigonometric Functions Are Rational," Discrete & Computational Geometry, 22(3), 1999 pp. 321–332.
Permanent Citation
"Rational Linear Combinations of Pure Geodetic Angles"
http://demonstrations.wolfram.com/RationalLinearCombinationsOfPureGeodeticAngles/
Wolfram Demonstrations Project
Published: March 7 2011