Reactive Scattering on a LEPS Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
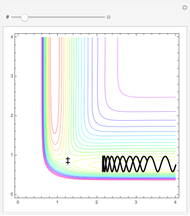
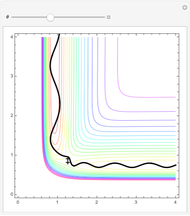
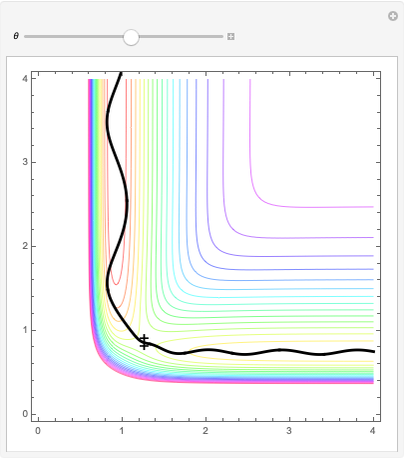
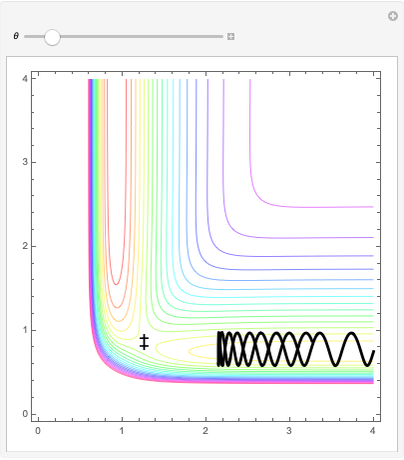
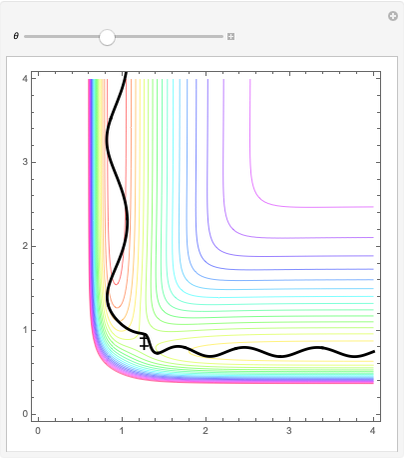
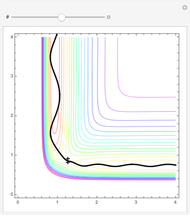
In this Demonstration, a model potential energy surface developed by London, Eyring, Polyani, and Sato (LEPS) is used to describe the collinear  chemical reaction. The particular parameterization is the "Muckerman V" potential. This potential surface is shown as a contour plot. The coordinates are the
chemical reaction. The particular parameterization is the "Muckerman V" potential. This potential surface is shown as a contour plot. The coordinates are the  and
and  bond lengths. The reaction proceeds with
bond lengths. The reaction proceeds with  being large and
being large and  being the equilibrium bond-length of
being the equilibrium bond-length of  The reaction path (which follows the contour minimum) connects the reactant channel to the product channel. These are separated by a saddle point that gives the configuration of the activated complex or transition state
The reaction path (which follows the contour minimum) connects the reactant channel to the product channel. These are separated by a saddle point that gives the configuration of the activated complex or transition state  which has energy
which has energy  -357.13 kcal/mol.
-357.13 kcal/mol.
Contributed by: Eric R. Bittner (University of Houston) (March 2011)
Funded in part by: National Science Foundation under grant CHE-0712981
Open content licensed under CC BY-NC-SA
Snapshots
Details
The modern theory of chemical reaction dynamics links the observed reaction rate to nuclear dynamics occurring on a potential energy surface. Potential energy surfaces are the connection between the quantum mechanical description of the electronic states of the system and the nuclear motion. The potential energy surfaces we will consider here are based upon the Born Oppenheimer approximation, which allows the separation of the motion of the electrons from the motion of the nuclei.
Here we solve the classical equations of motion describing the motion of the nuclei in the  collision complex to describe the
collision complex to describe the  chemical reaction.
chemical reaction.
One of the surprises is that simply having enough  does not ensure a reaction. Here we start a trajectory in the reactant channel with
does not ensure a reaction. Here we start a trajectory in the reactant channel with  just above
just above  and vary the initial velocity vector between
and vary the initial velocity vector between  and
and  . This changes the relative amount of energy partitioned to the translation of the incoming
. This changes the relative amount of energy partitioned to the translation of the incoming  atom and the vibrational energy of the initial
atom and the vibrational energy of the initial  molecule. When
molecule. When  , most of the energy is given to
, most of the energy is given to  atom translations and only these trajectories will proceed into the product channel. Here one can see the effect of an "early" transition state on the final energy distribution of product species.
atom translations and only these trajectories will proceed into the product channel. Here one can see the effect of an "early" transition state on the final energy distribution of product species.
For detailed descriptions of the Muckerman V potential and an in-depth treatment of reactive scattering please refer to:
P. L. Houston, Chemical Kinetics and Reaction Dynamics, Boston: McGraw Hill, 2001.
J. I. Steinfeld, J. S. Francisco, and W. L Hase, Chemical Kinetics and Dynamics, Englewood Cliffs, NJ: Prentice-Hall, 1989.
Permanent Citation