Real Roots of Sparse Polynomials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
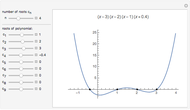
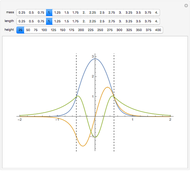
The number of real roots of a polynomial with  terms is bounded by
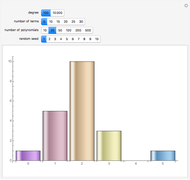
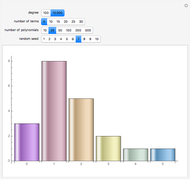
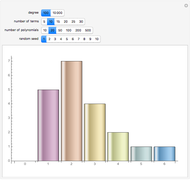
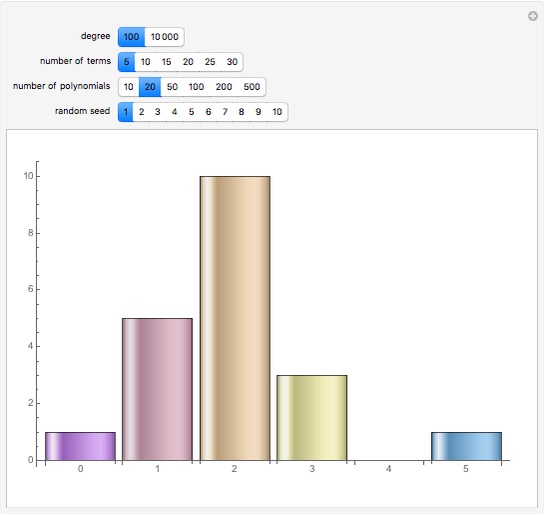
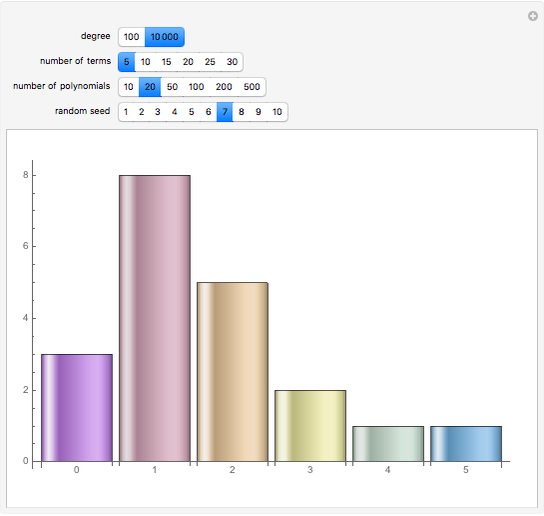
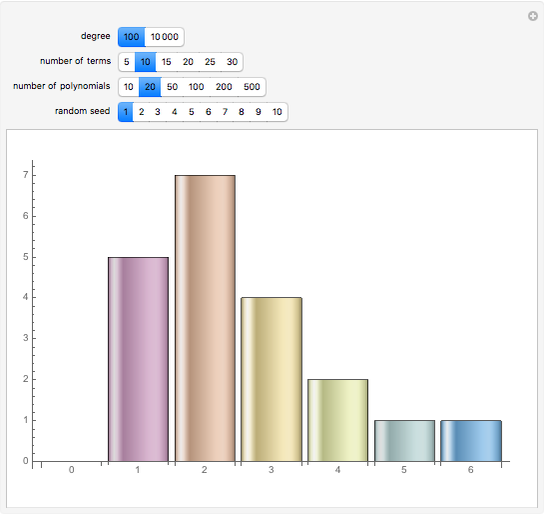
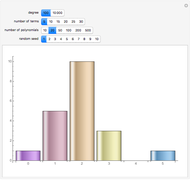
terms is bounded by  and does not depend on the degree of the polynomial. This chart shows the distribution of the number of real roots for 20 randomly generated polynomials of degree 100 with 10 terms each. If you keep the number of terms fixed and increase the degree to 10,000, the distribution of the number of real roots will be similar. With Mathematica 7 you can find real roots of polynomials with much higher degrees; however for polynomials of degree 1,000,000 generating the root distribution charts would take from a few seconds to about a minute per polynomial.
and does not depend on the degree of the polynomial. This chart shows the distribution of the number of real roots for 20 randomly generated polynomials of degree 100 with 10 terms each. If you keep the number of terms fixed and increase the degree to 10,000, the distribution of the number of real roots will be similar. With Mathematica 7 you can find real roots of polynomials with much higher degrees; however for polynomials of degree 1,000,000 generating the root distribution charts would take from a few seconds to about a minute per polynomial.
Contributed by: Adam Strzebonski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
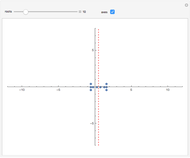
Polynomials used to generate the charts contain  terms with randomly generated integer coefficients between -1000 and 1000. The exponent of the leading term of each polynomial is randomly chosen to be either
terms with randomly generated integer coefficients between -1000 and 1000. The exponent of the leading term of each polynomial is randomly chosen to be either  or
or  ; the trailing term always has exponent zero and the exponents of the remaining
; the trailing term always has exponent zero and the exponents of the remaining  terms are a randomly generated sample of positive integers less than the leading exponent.
terms are a randomly generated sample of positive integers less than the leading exponent.
Permanent Citation