The Number of Distinct Real Roots of a Real Polynomial

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
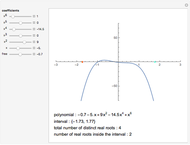
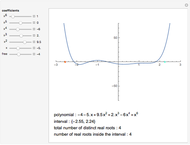
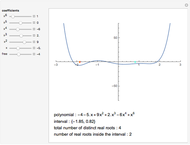
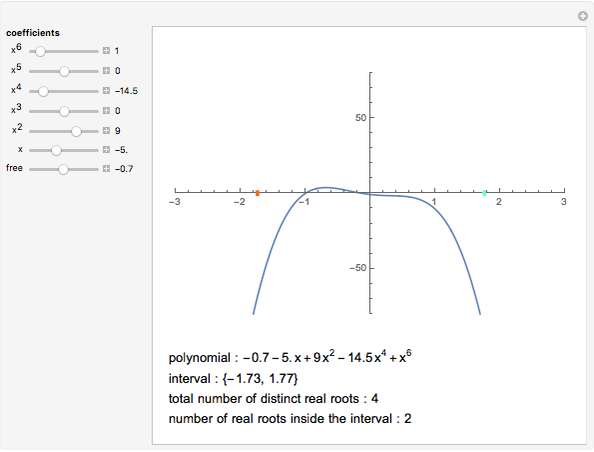
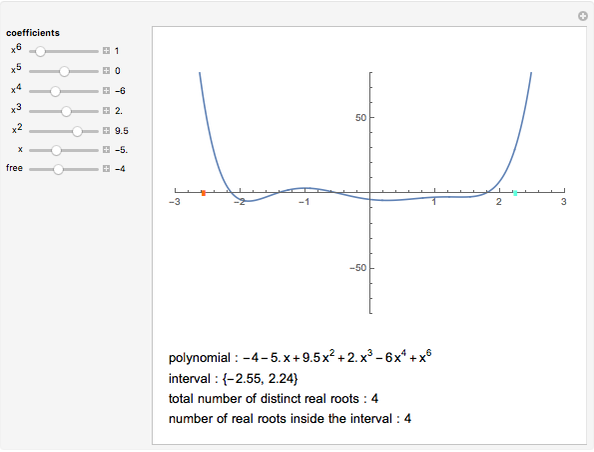
The problem of deciding if a real polynomial has a real root and if so, how many, has a long history going back to Descartes's Law of Signs. In more recent times substantial progress has been made in this area by several Chinese mathematicians. Here, some of their work is demonstrated: the computation of the number of distinct roots of a polynomial as well as the number of distinct roots lying in a given interval. The method is in the spirit of Descartes's Law of Signs and does not involve any root finding or root isolation.
[more]
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A method of completely determining the number and multiplicity of real roots of real polynomials with symbolic as well as numeric coefficients was given by Yang, Hou, and Zeng in [1]. The method can be seen as an extension of Descartes's Law of Signs: you compute the so-called "discriminant sequence" of the polynomial and count the number of sign changes among its nonzero terms. It is easy to use this method to compute the number of distinct roots in any interval. In this Demonstration, the total number of distinct real roots and the number of such roots lying in a chosen interval are shown. Yang, Hou, and Zeng actually do much more: they compute a "complete discrimination system" for a given polynomial with symbolic coefficients, which enables one to write explicit conditions in terms of the coefficients for the polynomial to have a given number of distinct real roots, to have multiple roots, etc.
[1] L. Yang, X. R. Hou, and Z. B. Zeng, "A Complete Discrimination System for Polynomials", Science in China, Series E, 39(6), 1996 pp. 628–646.
Permanent Citation