The Bifurcation Set of the Space of Smooth Real Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
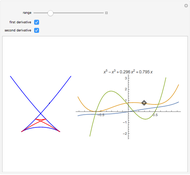
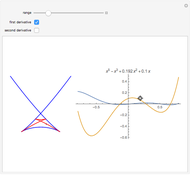
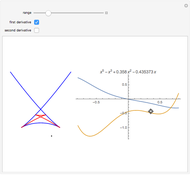
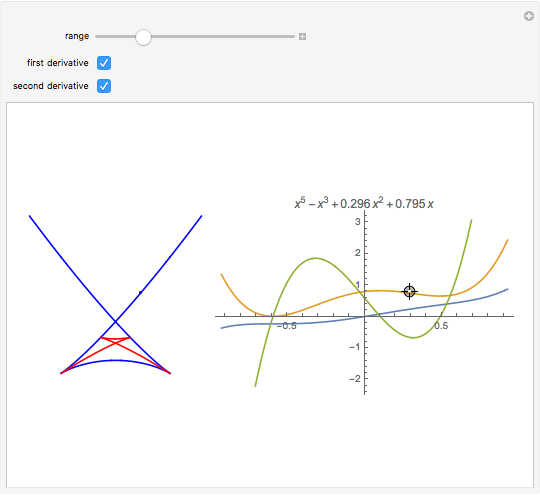
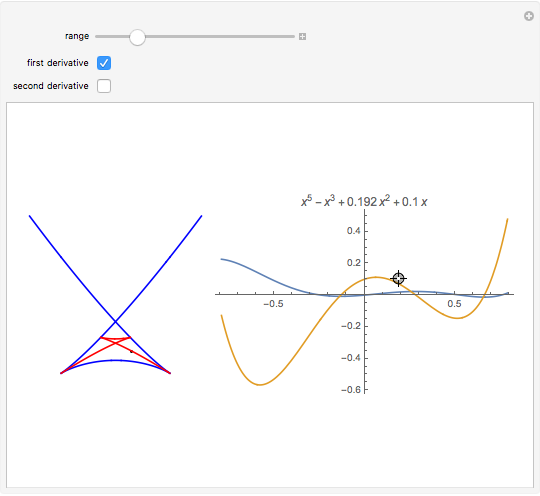
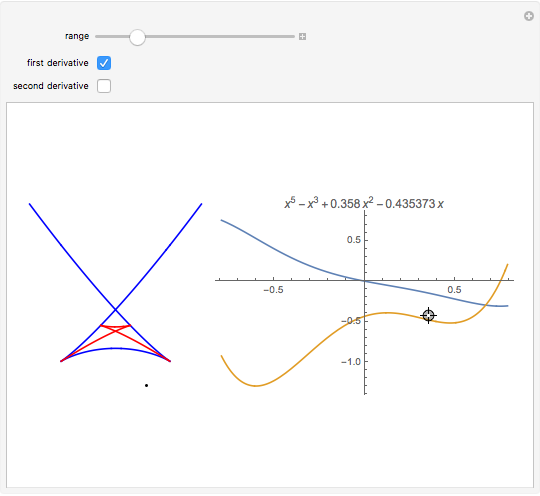
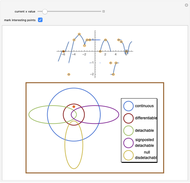
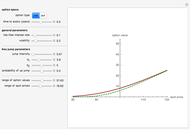
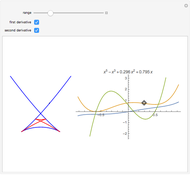
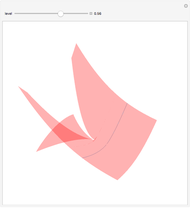
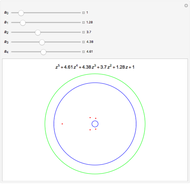
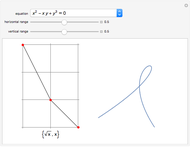
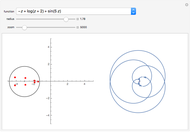
The diagram on the left shows the full bifurcation in the plane of the polynomials  . It consists of two hypersurfaces. The first, shown in blue, is called the caustic and consists of polynomials with degenerate critical points (both first and second derivatives vanish at the same point). The second, shown in red, is called the Maxwell set, and consists of polynomials with coinciding critical values. The full bifurcation set divides the plane into seven components of equivalent polynomials. The diagram on the right shows the graph of the polynomial chosen by the locator in the diagram on the left and, optionally, the graph of its first and second derivatives.
. It consists of two hypersurfaces. The first, shown in blue, is called the caustic and consists of polynomials with degenerate critical points (both first and second derivatives vanish at the same point). The second, shown in red, is called the Maxwell set, and consists of polynomials with coinciding critical values. The full bifurcation set divides the plane into seven components of equivalent polynomials. The diagram on the right shows the graph of the polynomial chosen by the locator in the diagram on the left and, optionally, the graph of its first and second derivatives.
Contributed by: Andrzej Kozlowski (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The example considered in this Demonstration illustrates some basic concepts in the theory of singularities of smooth real functions and is taken from p. 7 of [1].
Two functions  are considered equivalent if they can be transformed into one another by a smooth change of the independent and the dependent variables. A critical point of a function is a point at which the derivative of the function vanishes. Such a point is called nondegenerate if the second differential at the point is a nondegenerate quadratic form (for
are considered equivalent if they can be transformed into one another by a smooth change of the independent and the dependent variables. A critical point of a function is a point at which the derivative of the function vanishes. Such a point is called nondegenerate if the second differential at the point is a nondegenerate quadratic form (for  , this simply means the second derivative is nonzero).
, this simply means the second derivative is nonzero).
In the functional space of all functions, degenerate functions (those containing degenerate critical points) form a hypersurface (a submanifold of codimension 1) called the bifurcation set, which, in general, consists of smooth manifolds of different dimensions adjacent to each other in a special way.
The full bifurcation set consists of the caustic (in the corresponding optical problem, it is the set of points where light is concentrated) and the Maxwell set (because of the Maxwell rule in phase transition theory: coincidence of two critical values of some function).
A typical function has only nondegenerate critical points and its local structure is completely described by the Morse lemma. Globally, the set of critical points does not determine a function up to equivalence. However, if we remove the full bifurcation set, then two functions in the same component are equivalent. The full bifurcation set consists of six points and 10 intervals (two infinite ones).
It is clearly impossible to illustrate the complete space of smooth functions and its bifurcation set on a computer since they are infinite-dimensional. What one can do instead is to illustrate a finite-dimensional subspace in a way that captures the nature of the part of the bifurcation set that lies in specific codimensions. The space of polynomials considered here is a two-parameter subspace of the space of smooth functions: it is a two-dimensional submanifold of this infinite-dimensional space. The intersection of the space of polynomials considered here with the full bifurcation set is transversal. This implies that the picture of the bifurcation set in this Demonstration also provides a correct picture of the singularities of the bifurcation set of the space of functions lying in the strata of codimensions less or equal to 2.
Reference
[1] V. I. Arnold, The Theory of Singularities and Its Applications, New York: Lezioni Fermiane, 1993.
Permanent Citation