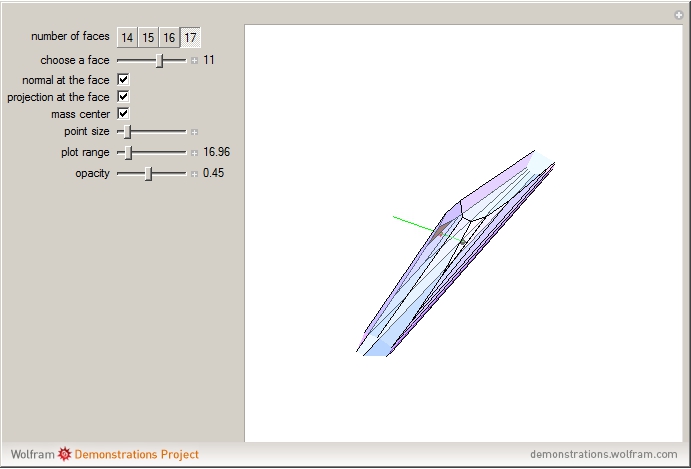
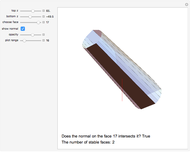
Reshetov's Unistable Polyhedra with 14, 15, 16, and 17 Faces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
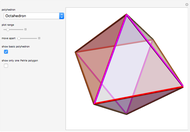
This Demonstration shows Reshetov's unistable polyhedra with 14, 15, 16, and 17 faces. A face  is stable if and only if the orthogonal projection (red point) of the center of mass (black point) onto
is stable if and only if the orthogonal projection (red point) of the center of mass (black point) onto  lies inside
lies inside  . Unistable polyhedron have only one stable face.
. Unistable polyhedron have only one stable face.
Contributed by: Izidor Hafner (April 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Guy constructed a unistable 19-face solid in 1968 [2, 3, 4]. Bezdek found a unistable solid with 18 faces in 2011 [1]. In [5] Reshetov constructed unistable polyhedra with 14, 15, 16, and 17 faces. Data and code are from [5].
References
[1] A. Bezdek, "On Stability of Polyhedra," Workshop on Discrete Geometry, Sep 13-16, 2011, Fields Institute, Toronto, Canada. www.fields.utoronto.ca/programs/scientific/11-12/discretegeom/talks/#discretegeom.
[2] J. Bryant and C. Sangwin, How Round Is Your Circle?: Where Engineering and Mathematics Meet, Princeton: Princeton University Press, 2008 pp. 273–276.
[3] R. K. Guy, A Unistable Polyhedron, Calgary: University of Calgary Department of Mathematics, 1968 (out of print).
[4] J. H. Conway, M. Goldberg, and R. K. Guy, "Problem 66-12," SIAM Review 11(1), 1969 pp. 78–82. doi:10.1137/1011014.
[5] A. Reshetov, "A Unistable Polyhedron with 14 Faces," International Journal of Computational Geometry & Applications, 24(1), 2014 pp. 39–60. doi:10.1142/S0218195914500022.
Permanent Citation