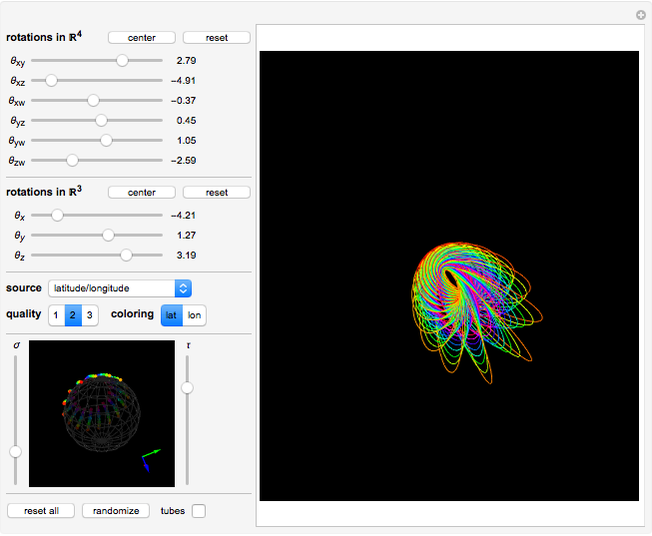
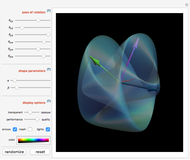
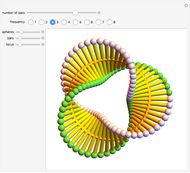
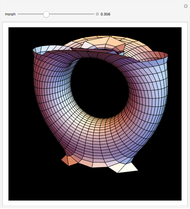
Rotating the Hopf Fibration

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
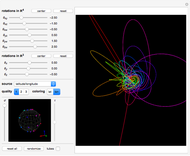
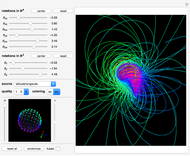
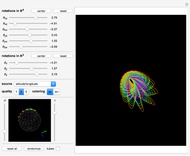
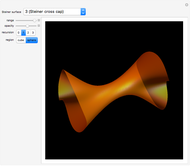
The Hopf fibration describes a relationship between the one-dimensional sphere  (a circle), the two-dimensional sphere
(a circle), the two-dimensional sphere  (an ordinary sphere), and the three-dimensional sphere
(an ordinary sphere), and the three-dimensional sphere  (a hypersphere in 4D space) as a fibration
(a hypersphere in 4D space) as a fibration  with
with  as the fiber,
as the fiber,  as the base space, and
as the base space, and  as the total space. This mapping has the property that when viewed locally,
as the total space. This mapping has the property that when viewed locally,  is indistinguishable from the Cartesian product
is indistinguishable from the Cartesian product  . However, this is not true globally, since a fibration has a "twist" that distinguishes it from a regular product space.
. However, this is not true globally, since a fibration has a "twist" that distinguishes it from a regular product space.
Contributed by: Richard Hennigan (March 2011)
Open content licensed under CC BY-NC-SA
Details
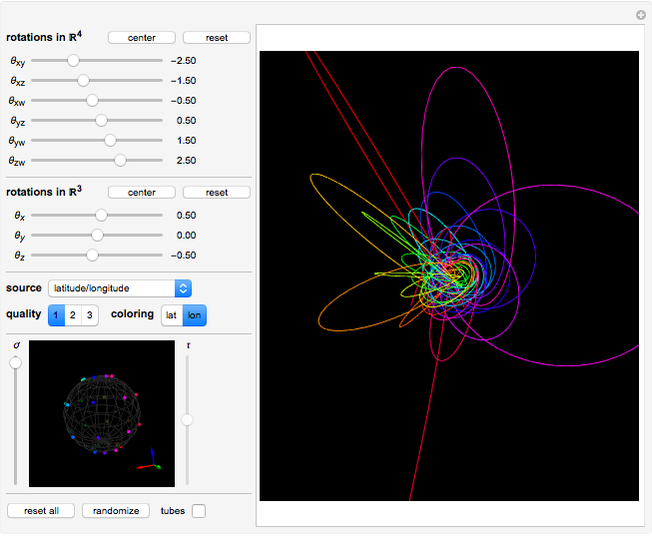
While manipulating this Demonstration, here are some features of the Hopf fibration (and  in general) to look for:
in general) to look for:
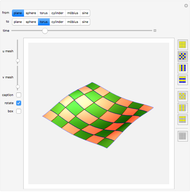
• In the stereographic projection, points closer to the north pole of  are mapped to larger circles, with the north pole itself mapping to a circle of infinite radius, resulting in a straight line.
are mapped to larger circles, with the north pole itself mapping to a circle of infinite radius, resulting in a straight line.
• Any given pair of circles are linked together in what is known as a Hopf link.
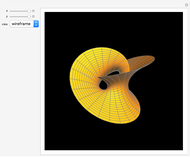
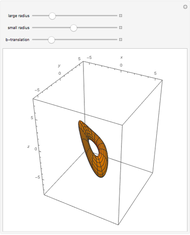
• The parallels of  are mapped to nested tori (use the
are mapped to nested tori (use the  slider to compress points to a circle).
slider to compress points to a circle).
• A torus embedded in  can be turned inside out without intersecting itself.
can be turned inside out without intersecting itself.
Snapshots
Permanent Citation