The Topology of Costa's Minimal Surface

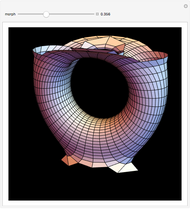
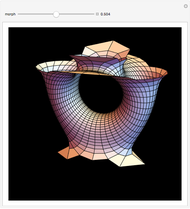
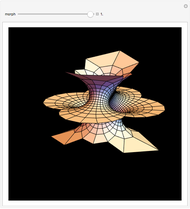
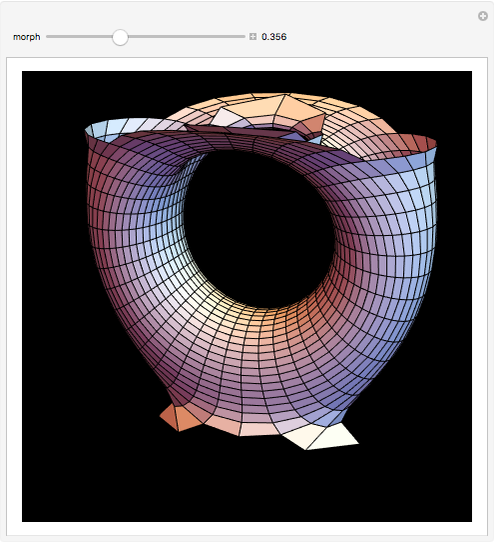
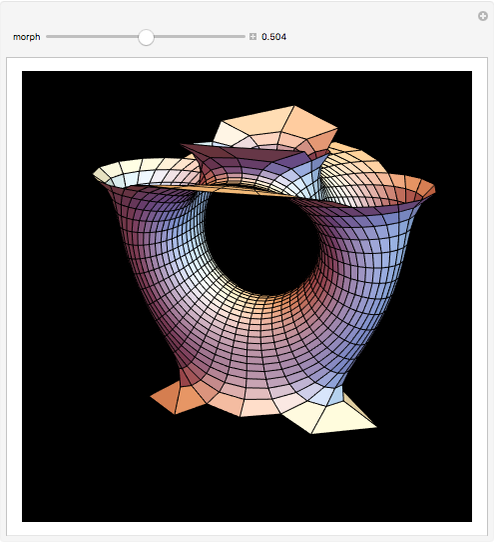
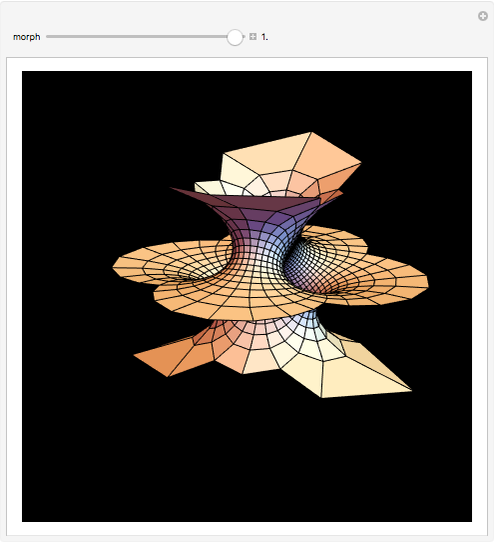
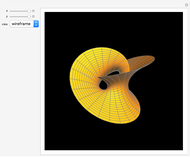
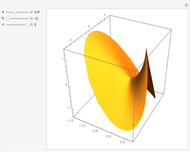
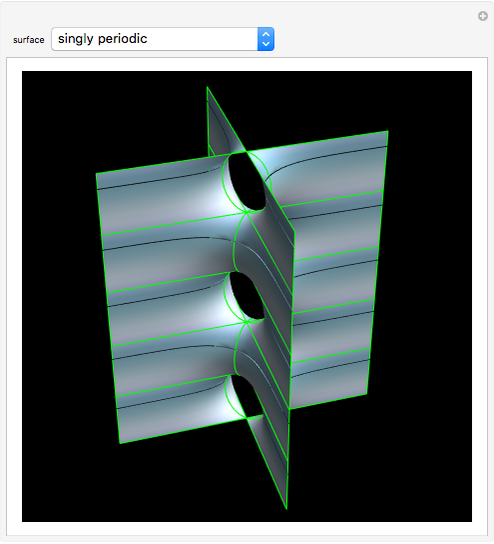
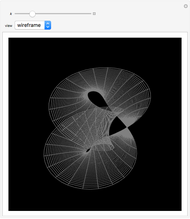
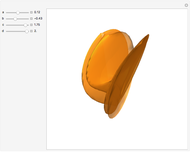
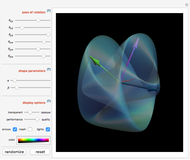
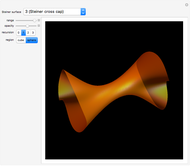
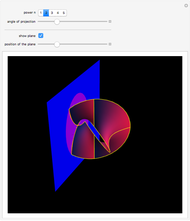
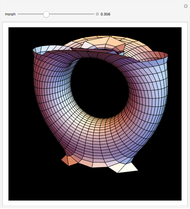
Costa's minimal surface is described as a torus with three points removed. How is this done? The points are literally removed from 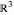and flung to infinity. Here is a Demonstration of specifically where on the torus the points are removed and how the torus turns itself inside-out when the resulting ends of the surface are flung to infinity.