Shortest Path between Two Points in the Unit Disk Reflecting off the Circumference

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
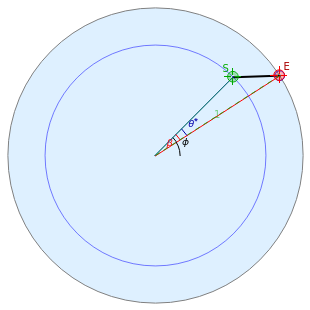
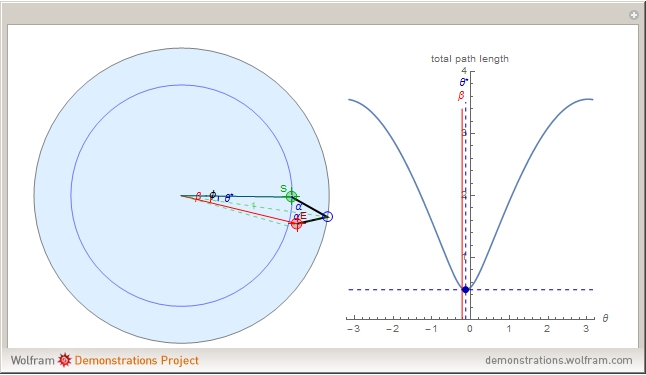
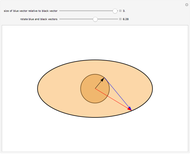
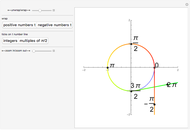
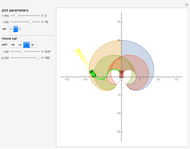
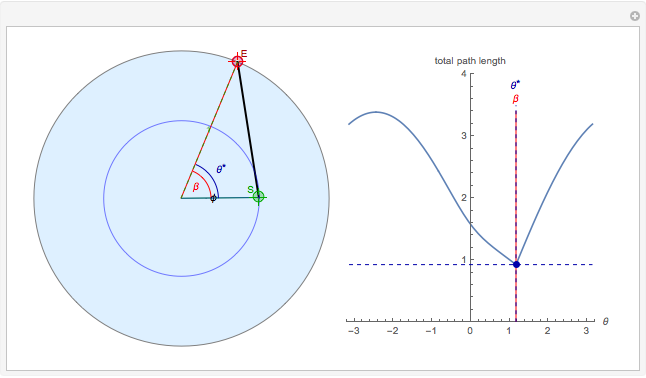
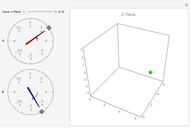
Given two points within the unit disk labeled 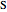 (in green) and
(in green) and  (in red), what is the shortest path between the two points that reflects off the unit circle? You can drag the two points.
(in red), what is the shortest path between the two points that reflects off the unit circle? You can drag the two points.
Contributed by: Jingang Shi and Aaron T. Becker (September 2017)
(University of Houston)
Open content licensed under CC BY-NC-SA
Snapshots
Details
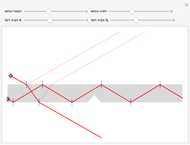
The shortest path between two points in the unit disk that reflects off the circumference is composed of two straight line segments. The problem can be simplified by choosing the coordinate system carefully. We define the  axis along the position of the starting point:
axis along the position of the starting point: 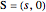 , and define the point of intersection by the angle
, and define the point of intersection by the angle  from the
from the  axis
axis 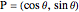 , and the final point by a radius
, and the final point by a radius  and angle
and angle 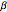 ,
, 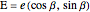 . Then define a symmetry point about
. Then define a symmetry point about 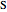 of line
of line 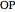 named
named  .
.
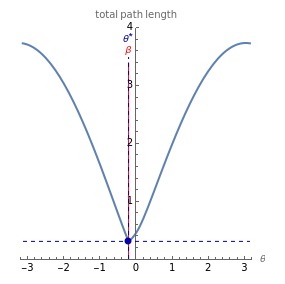
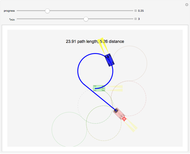
Then the length of the two line segments is
 ,
,
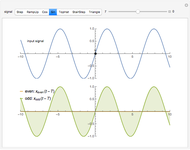
which is minimized by choosing an appropriate  value. This equation can be simplified to
value. This equation can be simplified to
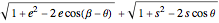 .
.
The length of the two line segments as a function of  is drawn in the right plot.
is drawn in the right plot.
There are several simple solutions. If  is 1 or
is 1 or  is 0 or
is 0 or 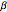 is 0, the optimal angle
is 0, the optimal angle 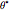 is 0. If
is 0. If  is 1 or
is 1 or  is 0, the optimal angle is
is 0, the optimal angle is 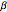 .
.
Label the origin  . The optimal solution shows that the angle
. The optimal solution shows that the angle  (from the origin to
(from the origin to  to
to  ) is the same as the angle
) is the same as the angle  (from the origin to
(from the origin to 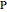 to
to  ).
).
We name these angles  . This can be proved by drawing an ellipse whose foci are
. This can be proved by drawing an ellipse whose foci are 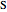 and
and  . When the ellipse is tangent to the circle, the point of tangency is exactly
. When the ellipse is tangent to the circle, the point of tangency is exactly 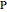 .
.
Since the distance from the origin to 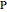 is always 1, we can set up three equalities using the law of sines:
is always 1, we can set up three equalities using the law of sines:
From triangle 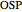 :
: 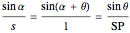 .
.
From triangle 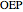 :
: 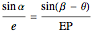 .
.
If we mirror the point 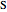 about the
about the  axis and label this point
axis and label this point  , from triangle
, from triangle 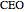 :
: 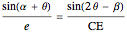 .
.
Simplifying this system of equations results in: 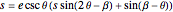 .
.
Solving this last equation results in a quartic solution that has a closed-form solution with four roots, each of which can be either a clockwise or a counterclockwise rotation  , depending on the sign of
, depending on the sign of 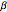 , with
, with  . We evaluate each and select the solution that results in the shortest length path.
. We evaluate each and select the solution that results in the shortest length path.
Note that the optimal path satisfies the law of reflection off the unit circle, with angle of incidence equal to angle of reflection.
Permanent Citation