Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Singular Values in 2D

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

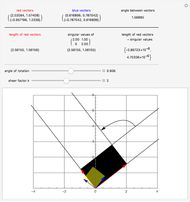
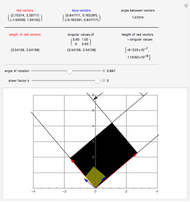
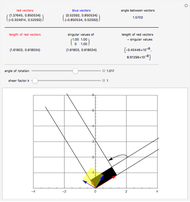
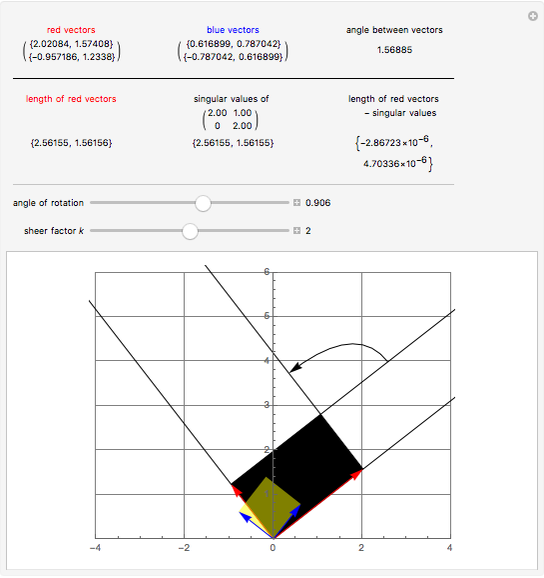
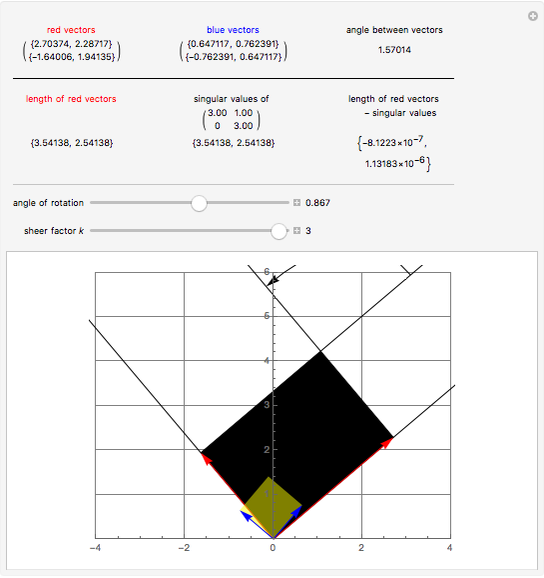
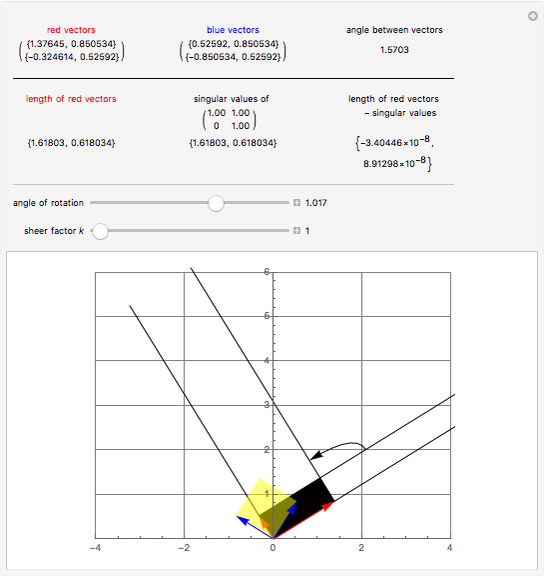
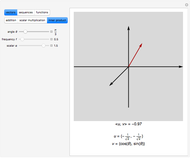
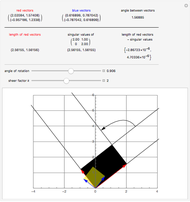
Some square matrices are diagonalizable or even orthogonally diagonalizable. An important fact about diagonalization is that the resulting diagonal matrix contains the eigenvalues of the original matrix on the main diagonal. However, not all matrices are diagonalizable. In such a case, the singular value decomposition (SVD) still exists. If is an matrix, its singular values are the square roots of the eigenvalues of the matrix .

[more]

The term singular value relates to the distance of the given matrix to a singular matrix. The idea behind SVD is that every matrix can be decomposed into a product , where and are orthogonal matrices and and .

This Demonstration shows the singular values of certain linear transformations in , including rotation, dilation, and the sheer transformation of factor . The yellow square (with blue arrows) is the original region and the black region (with red arrows) is the transformed region. The singular values of the standard matrix affiliated with the transformation can be found when the transformed grid is orthogonal.

Choose a transformation and rotation of the grid until it appears to be orthogonal; the length of the red arrows approaches the singular values of the standard matrix.

[less]

Contributed by: Crista Arangala (March 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send