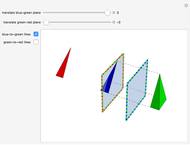
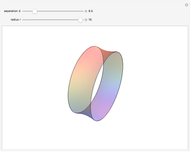
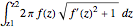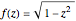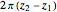Slicing a Sphere along Two Parallel Planes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
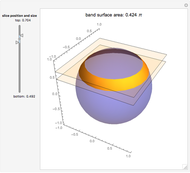
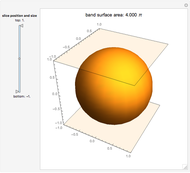
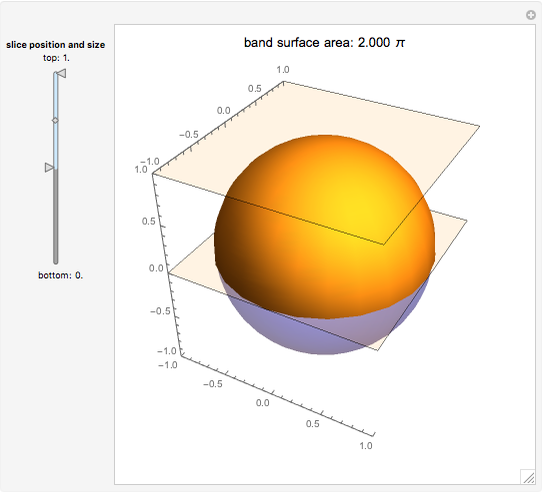
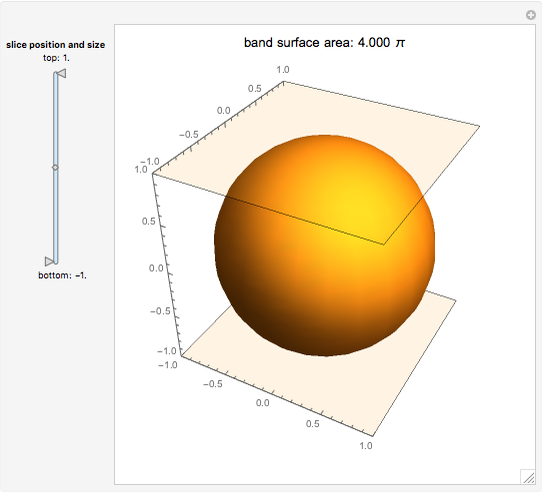
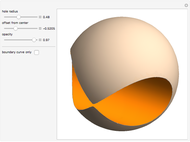
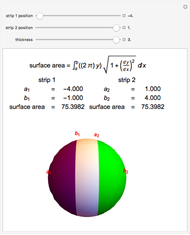
In their book Calculus, One and Several Variables [1], Salas and Hille mention "an interesting property of the sphere" and propose the following exercise:
[more]
Contributed by: Erik Mahieu (November 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] S. L. Salas and E. Hille, Chapter 10.10, problem 25, Calculus: One and Several Variables, 6th ed., New York: John Wiley and Sons, 1990.
Permanent Citation
"Slicing a Sphere along Two Parallel Planes"
http://demonstrations.wolfram.com/SlicingASphereAlongTwoParallelPlanes/
Wolfram Demonstrations Project
Published: November 24 2015