Smallest Circle Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
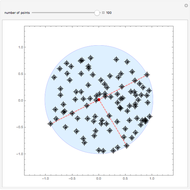
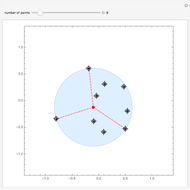
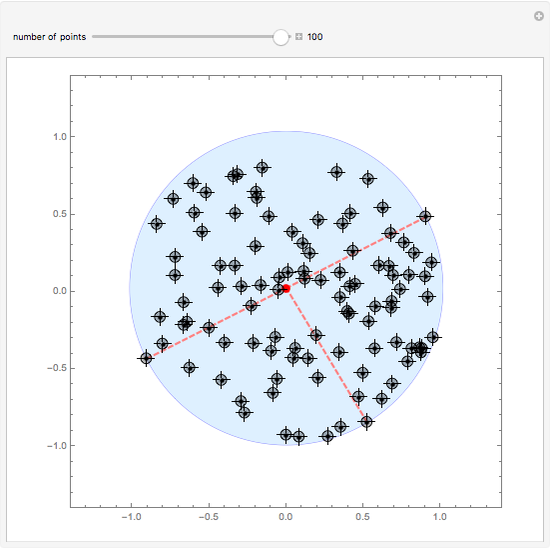
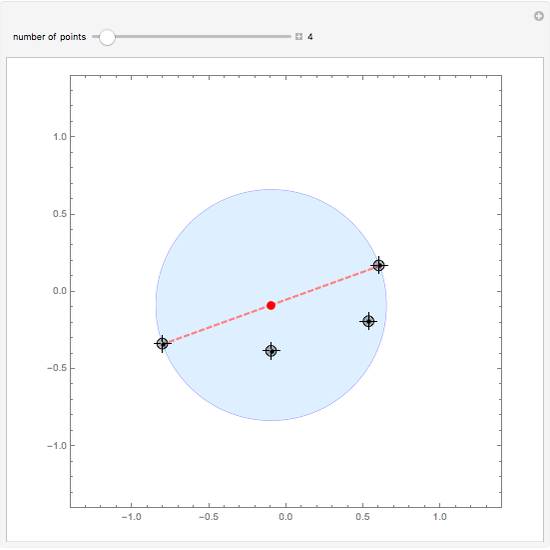
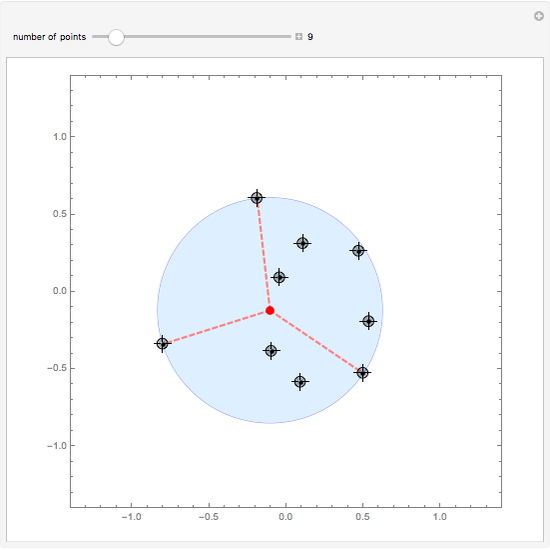
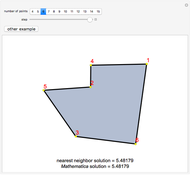
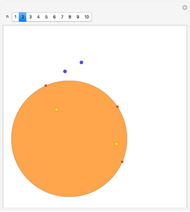
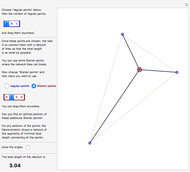
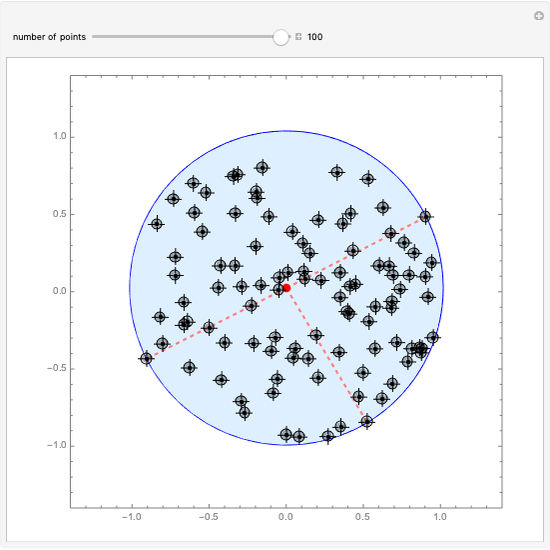
The smallest circle problem for a set of two-dimensional points seeks to find the smallest-radius circle that contains all the points. This Demonstration uses the Matoušek, Sharir and Welzl (MSW) algorithm [1] that computes the circle for  points in expected
points in expected  time. Move the locators to interact with the solution and use the slider to change the number of points.
time. Move the locators to interact with the solution and use the slider to change the number of points.
Contributed by: Mohammad Sultan and Aaron T. Becker (December 2019)
Open content licensed under CC BY-NC-SA
Details
The smallest circle problem is also known as the minimum covering circle problem, bounding circle problem or smallest enclosing circle problem. For  points, a naive solution runs in
points, a naive solution runs in  time, but this randomized algorithm runs in expected linear time, using the MSW algorithm [1]. This recursive algorithm builds and corrects the bounding circle. It returns the minimum circle
time, but this randomized algorithm runs in expected linear time, using the MSW algorithm [1]. This recursive algorithm builds and corrects the bounding circle. It returns the minimum circle  , with circle center
, with circle center  and the radius
and the radius  . See the initialization code for implementations of the functions msw, trivialMinCircle and nonbase.
. See the initialization code for implementations of the functions msw, trivialMinCircle and nonbase.
msw algorithm:
input: finite sets  and
and  of points in the plane,
of points in the plane,  output: minimal disk enclosing
output: minimal disk enclosing  if
if  is empty
return trivialMinCircle(
is empty
return trivialMinCircle( )
choose
)
choose  (randomly and uniformly)
(randomly and uniformly)

 if
if  :
:
 return
return 
Reference
[1] J. Matsuoka, M. Sharir and E. Welzl, "A Subexponential Bound for Linear Programming," Algorithmica, 16(4–5), 1996 pp. 498–516. doi:10.1007/BF01940877.
Snapshots
Permanent Citation