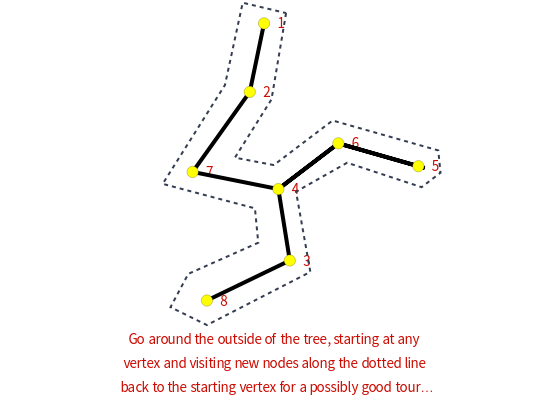
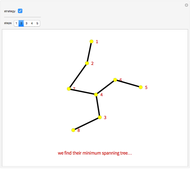
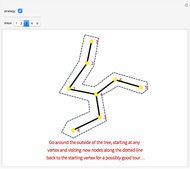
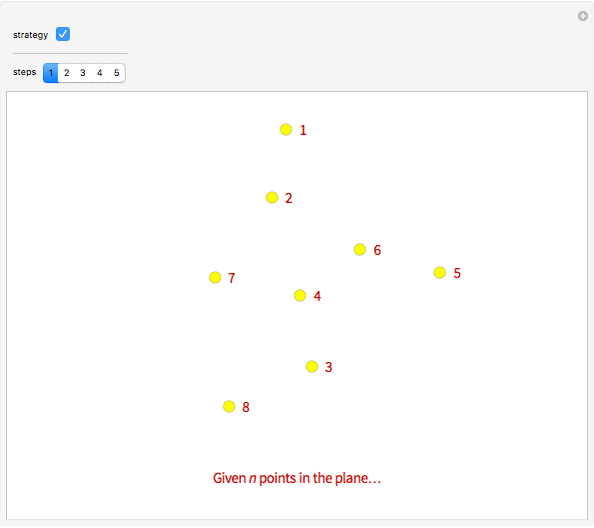
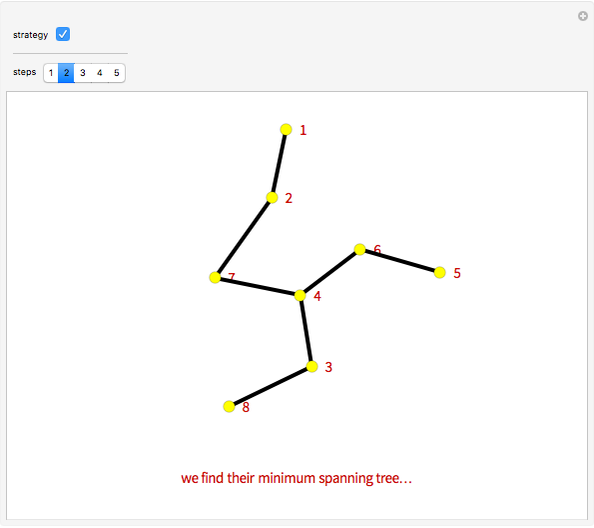
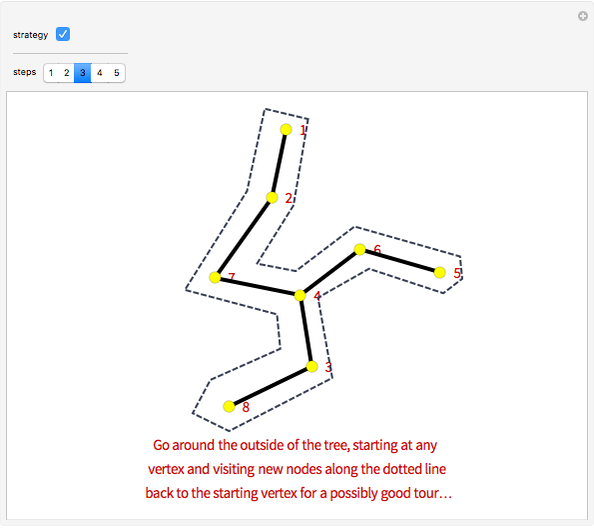
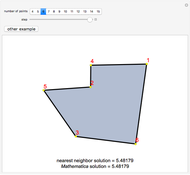
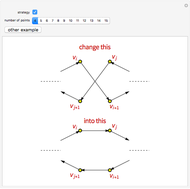
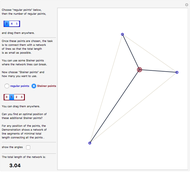
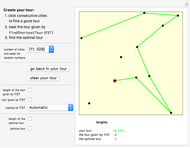
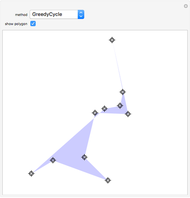
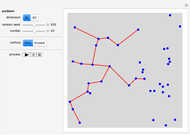
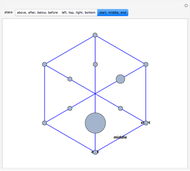
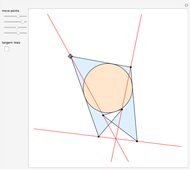
The traveling salesman problem is NP-hard, that is, there is no polynomial-time algorithm that solves it. Instead, we look for approximation algorithms based on heuristic (common sense) rules. One of the easiest to state is the following: obtain the minimum spanning tree of the given points (with Kruskal's algorithm or Prim's algorithm) and then traverse it in preorder (in which we visit the root first and then recursively do a preorder traversal of each of its subtrees). As we can choose the root of the tree to be any point, there are several possible answers. Choose the best of them. The solutions obtained by this method are of length at most twice the optimal. Because of its speed, it can be used with other heuristics, for example 2-opt, to improve the result.