Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

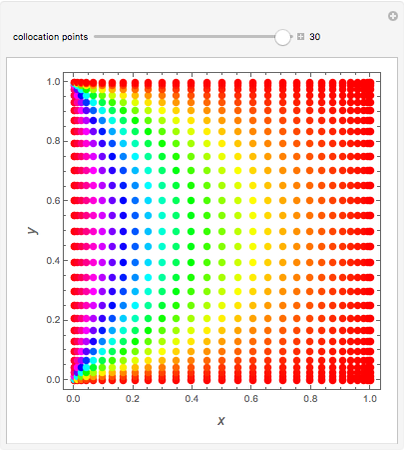
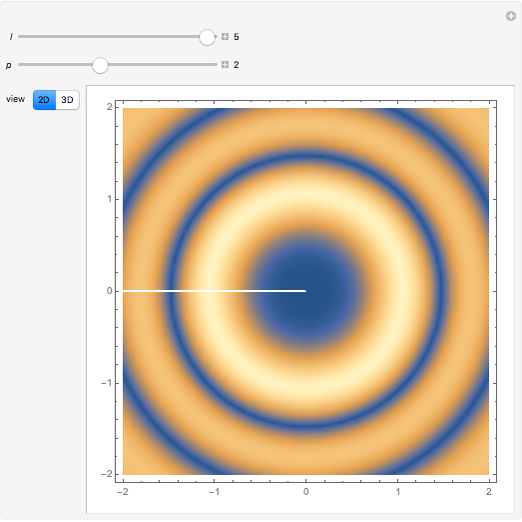
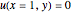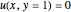Solution of the Laplace Equation for Temperature Distribution in a Square

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

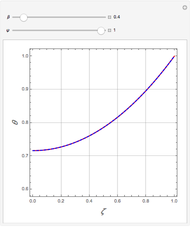
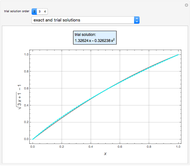
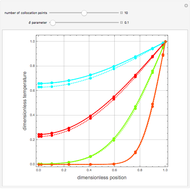
Consider the Laplace equation in a square region, where 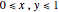. We wish to solve for the temperature distribution 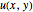, subject to the following Dirichlet boundary conditions:

[more]

BC1: ,

BC2: ,

BC3: ,

BC4: .

This Demonstration solves the problem using a spectral method [1] for a user-set value of the number of the Chebyshev–Gauss–Lobatto collocation points. The colored dots reflect the intensity of the scalar field at the various nodes in the square domain. You can clearly recognize the form of a contour plot of in the third snapshot.

[less]

Contributed by: Housam Binous and Ahmed Bellagi (August 2015)
Open content licensed under CC BY-NC-SA

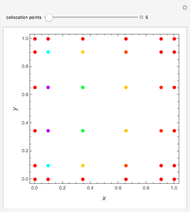
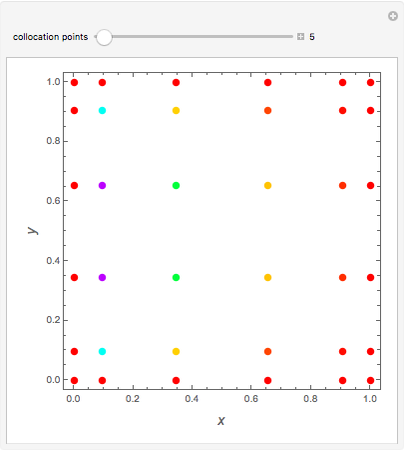
Snapshots

Details

Reference

[1] L. N. Trefethen, Spectral Methods in MATLAB, Philadelphia: SIAM, 2000.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send