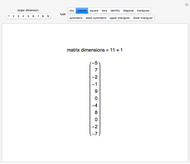
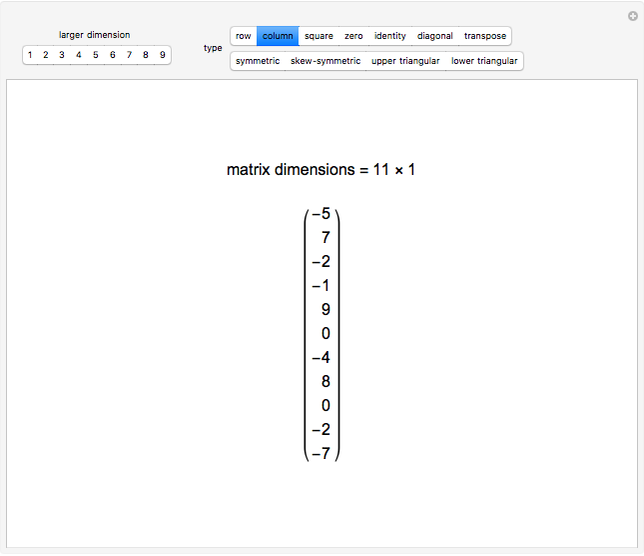
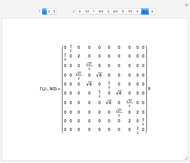
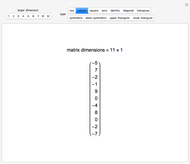
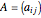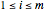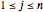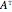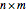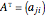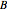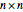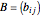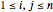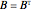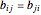If there is only one row or column, the matrix can be treated like a vector.
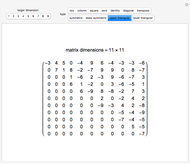
For a square matrix, the number of rows equals the number of columns.
A zero matrix acts like the number zero for matrices of the same dimensions.
The main diagonal of a square matrix runs from the top-left corner to the bottom-left corner.
The identity matrix is square, with ones on the main diagonal and zeros elsewhere. It acts like the number one for matrix multiplication.
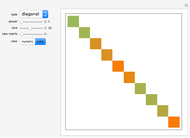
A diagonal matrix is a square matrix that has zeros off the main diagonal.
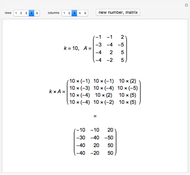
Let 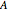 be
be 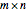 and
and 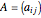 , where
, where 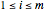 and
and 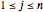 .
.
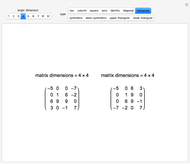
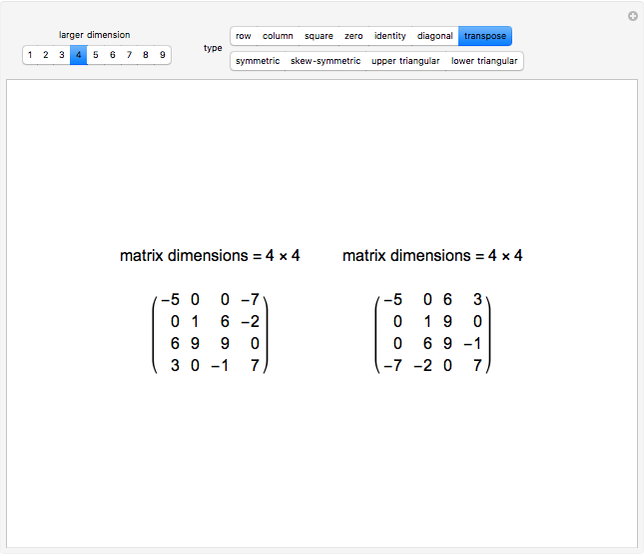
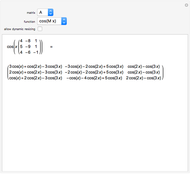
The transpose of the matrix 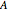 , written
, written 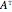 , reverses the rows and columns of
, reverses the rows and columns of 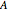 , so that
, so that 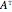 is
is 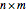 and
and 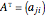 . Another way to think of
. Another way to think of 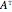 is as the reflection of
is as the reflection of 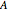 in its main diagonal.
in its main diagonal.
Let 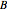 be an
be an 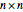 square matrix and
square matrix and 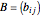 , where
, where 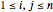 .
.
A square matrix 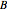 is symmetric if
is symmetric if 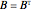 , so that
, so that 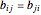 .
.
A square matrix 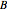 is skew-symmetric if
is skew-symmetric if  , so that
, so that  . A skew-symmetric matrix is therefore zero on the main diagonal.
. A skew-symmetric matrix is therefore zero on the main diagonal.
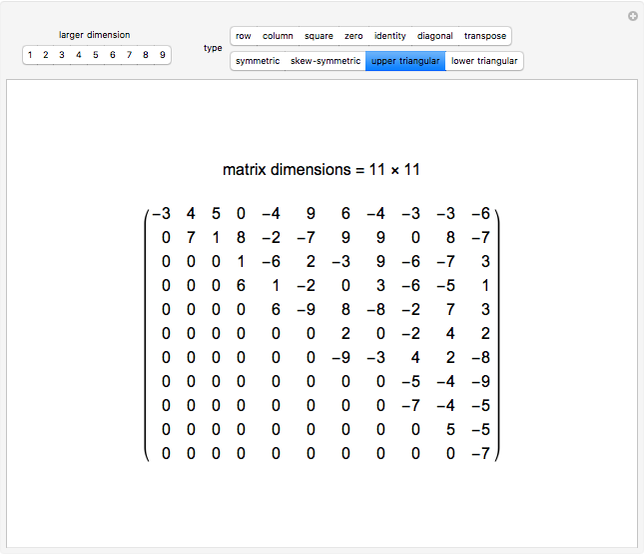
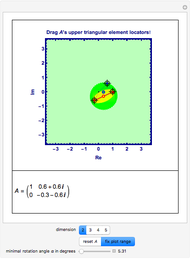
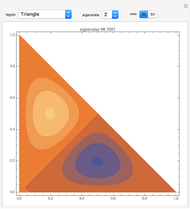
A square matrix 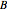 is upper triangular if it is zero below the main diagonal.
is upper triangular if it is zero below the main diagonal.
A square matrix 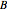 is lower triangular if it is zero above the main diagonal.
is lower triangular if it is zero above the main diagonal.
[less]

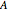 is
is 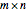 if it has
if it has 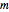 rows and
rows and  columns.
columns.