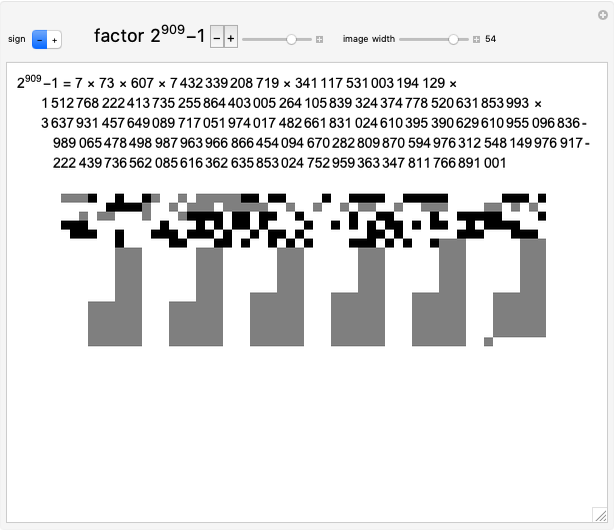
Sparse Rulers
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
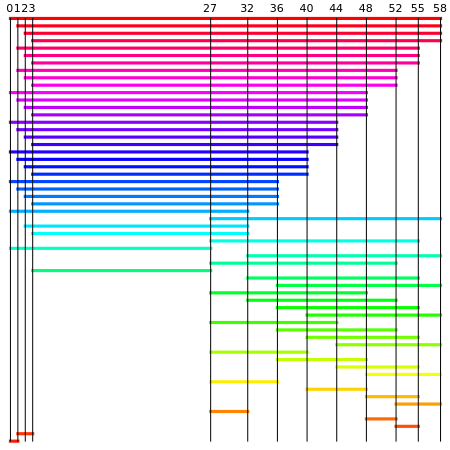
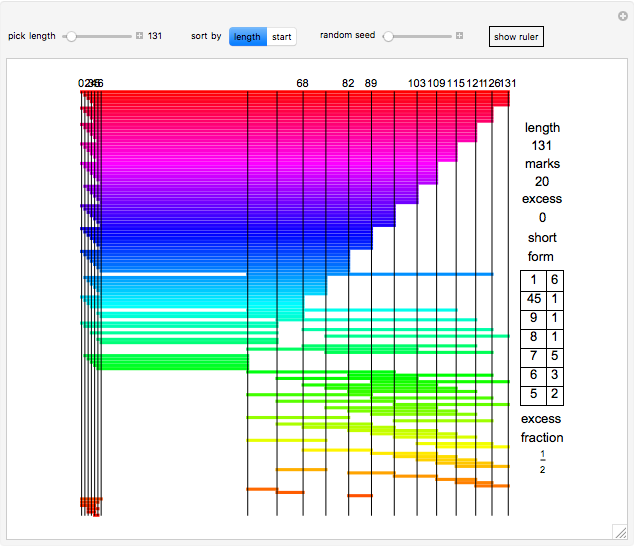
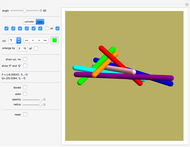
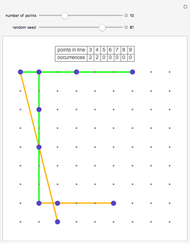
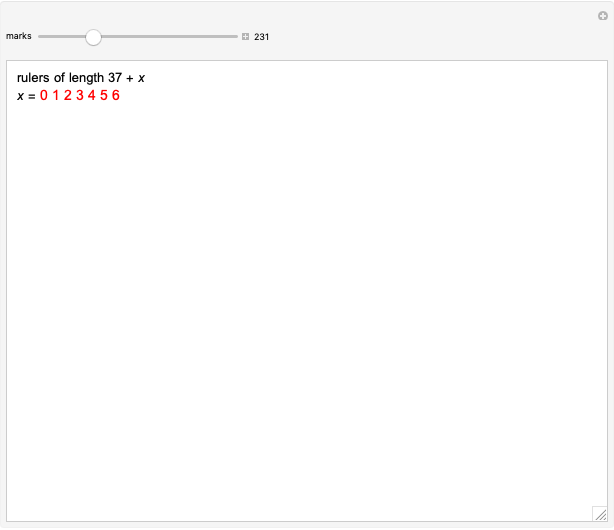
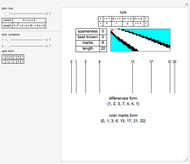
A sparse ruler is a rod of integer length  with a minimal number of marks so that all distances 1 to
with a minimal number of marks so that all distances 1 to  can be measured. Many lengths, such as 36, have unique rulers with a twin by subtracting marks from
can be measured. Many lengths, such as 36, have unique rulers with a twin by subtracting marks from  , as seen here:
, as seen here:
Contributed by: Ed Pegg Jr (June 2019)
Open content licensed under CC BY-NC-SA
Details
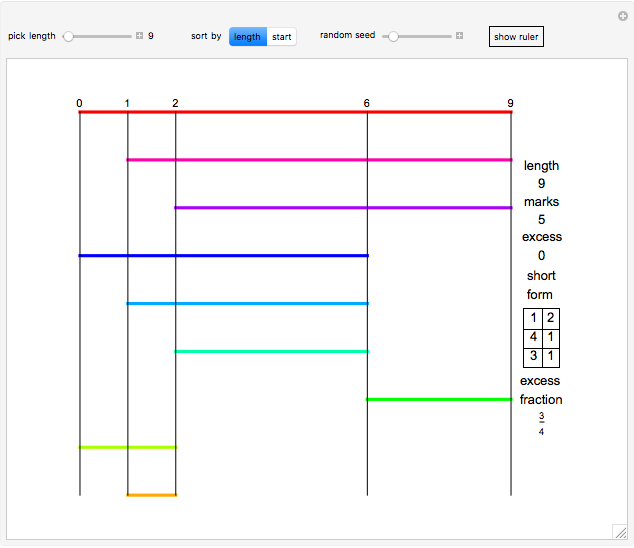
Snapshot 1: a simple case with extra marks at 1, 2 and 4 on a ruler of length 7; all the lengths from 1 to 7 can be measured as  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  .
.
Snapshots
Permanent Citation