Wichmann-like Rulers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
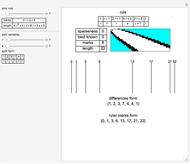
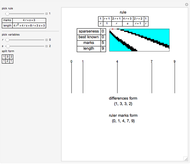
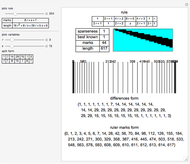
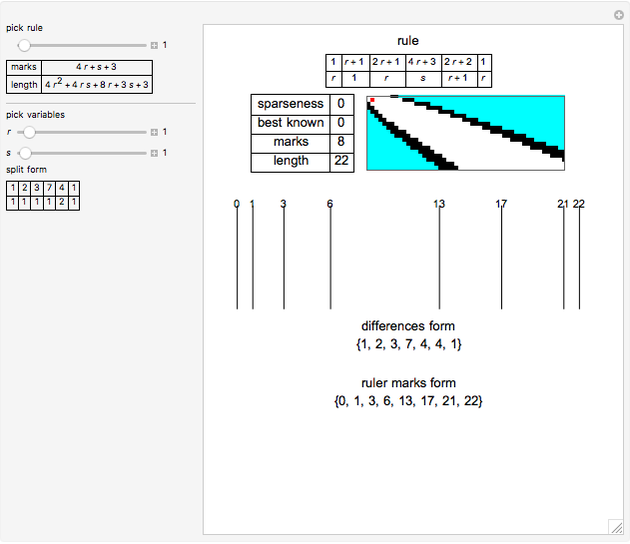
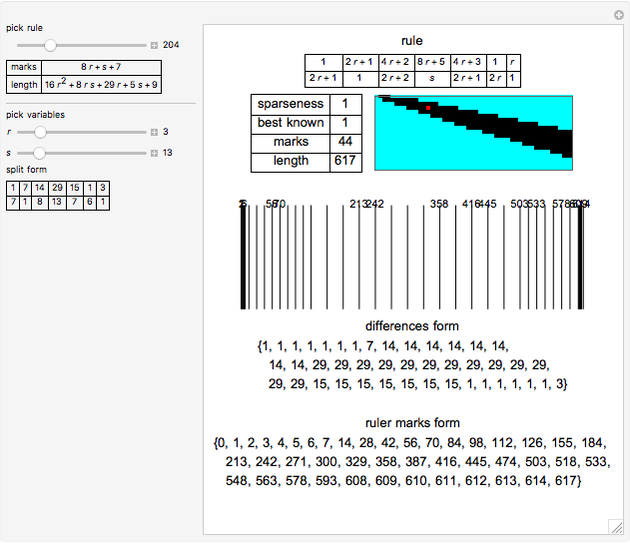
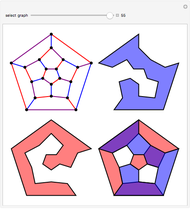
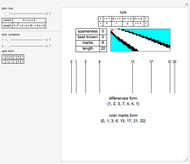
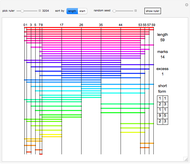
A sparse ruler is a rod of integer length  with a minimal number of marks
with a minimal number of marks  so that all distances 1 to
so that all distances 1 to  can be measured. With 1 to 9, its five marks are at
can be measured. With 1 to 9, its five marks are at  with differences between marks
with differences between marks  . The differences 1 to 9 are
. The differences 1 to 9 are  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Contributed by: Ed Pegg Jr (August 2019)
Open content licensed under CC BY-NC-SA
Details
References
[1] B. Wichmann, "A Note on Restricted Difference Bases," Journal of the London Mathematical Society, s1-38(1), 1963 pp. 465–466. doi:10.1112/jlms/s1-38.1.465.
[2] A. D. Robison. "Parallel Computation of Sparse Rulers." (Aug 7, 2019) software.intel.com/en-us/articles/parallel-computation-of-sparse-rulers.
[3] P. Luschny. "Perfect and Optimal Rulers." (Aug 7, 2019) oeis.org/wiki/User:Peter_Luschny/PerfectRulers.
Snapshots
Permanent Citation