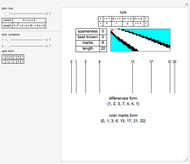
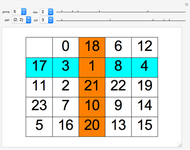
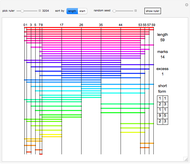
Wichmann Columns

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
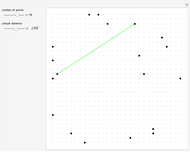
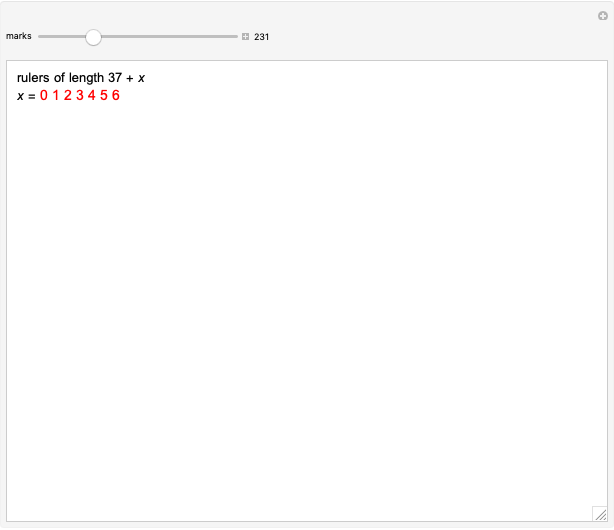
Much of the following explanation comes from the Demonstrations Wichmann-like Rulers [1] and Sparse Rulers [2].
[more]
Contributed by: Ed Pegg Jr (January 2020)
Open content licensed under CC BY-NC-SA
Details
References
[1] E. Pegg Jr. "Wichmann-like Rulers" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/WichmannLikeRulers.
[2] E. Pegg Jr. "Sparse Rulers" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/SparseRulers.
[3] B. Wichmann, "A Note on Restricted Difference Bases," Journal of the London Mathematical Society, s1–38(1), 1963 pp. 465–466. doi:10.1112/jlms/s1-38.1.465.
Snapshots
Permanent Citation