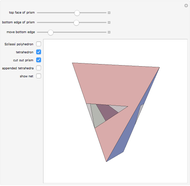
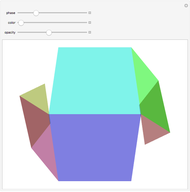
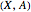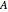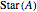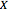Star Neighborhoods in Double Barycentric Subdivision

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration illustrates skeleta of stars and the dual of the double barycentric subdivision of a 3-simplex.
[more]
Contributed by: Aleksandr Berdnikov (August 2018)
Open content licensed under CC BY-NC-SA
Details
A significant number of topological spaces are (or can be modeled by) simplicial complexes—spaces that are "glued" out of simplexes, attaching them face to face. Given a subcomplex  of a complex
of a complex  , one would often like to consider a neighborhood
, one would often like to consider a neighborhood  of
of 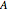 in
in 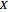 that approximates
that approximates 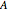 fairly well. It is not always possible to build such a
fairly well. It is not always possible to build such a  out of simplexes of
out of simplexes of  ; For example, if
; For example, if 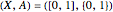 , the only simplicial neighborhood of
, the only simplicial neighborhood of  is the whole segment
is the whole segment  , which fails to capture the disconnectedness of
, which fails to capture the disconnectedness of 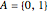 .
.
However, there are such neighborhoods that are simplicial in a double barycentric subdivision 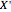 of
of  (i.e. each simplex is subdivided barycentrically twice). Given any subcomplex
(i.e. each simplex is subdivided barycentrically twice). Given any subcomplex 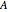 of
of  , such a neighborhood is given by
, such a neighborhood is given by  in
in  , where
, where 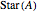 is defined as the union of all open simplexes with a vertex in
is defined as the union of all open simplexes with a vertex in  .
.
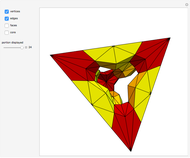
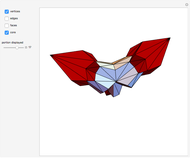
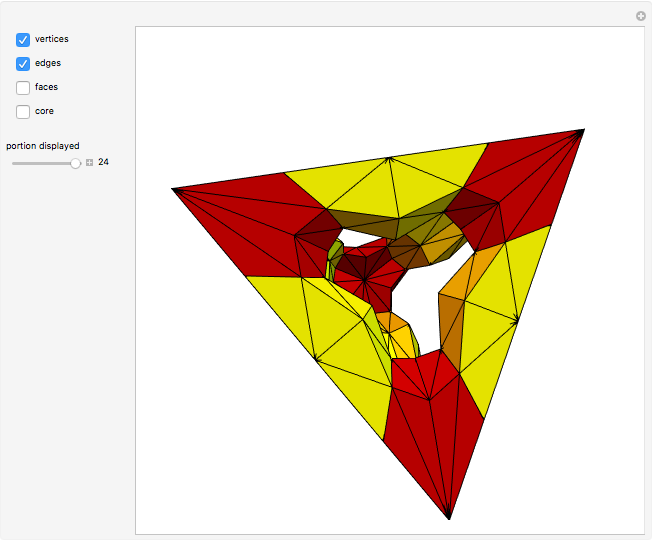
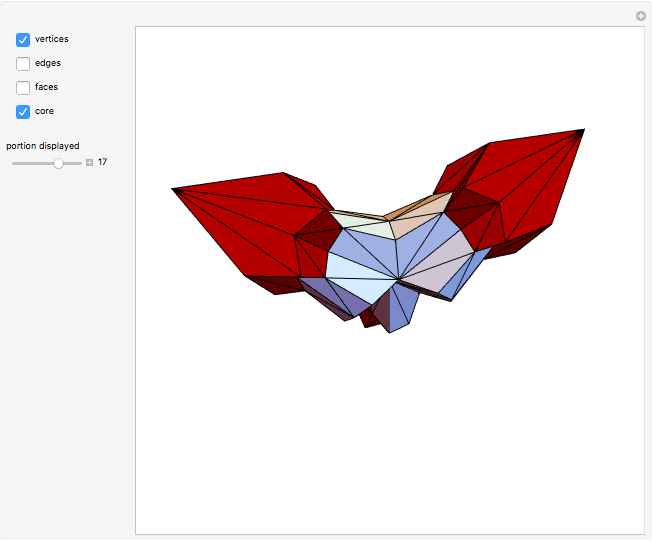
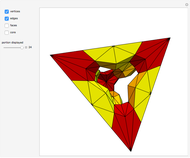
The Demonstration illustrates this concept with the 3-simplex as an example of  . Each controller toggles the display of stars (in the double subdivision) of centers of corresponding elements. For example, selecting "vertices" and "edges" gives a neighborhood of a 1-skeleton of
. Each controller toggles the display of stars (in the double subdivision) of centers of corresponding elements. For example, selecting "vertices" and "edges" gives a neighborhood of a 1-skeleton of 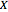 (i.e. of the collection of its 1-simplexes).
(i.e. of the collection of its 1-simplexes).
Barycentric subdivision is defined inductively. Subdivision of a point is the point itself. To define a subdivision  of a simplex
of a simplex  , take the subdivision
, take the subdivision 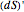 of its boundary
of its boundary  and take
and take  as the collection of simplexes with base the simplex in
as the collection of simplexes with base the simplex in  and vertex the barycenter of
and vertex the barycenter of  .
.
Snapshots
Permanent Citation