Substitution System Defined by Splitting Each Cell into Nine

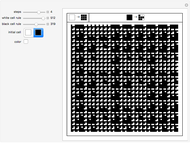
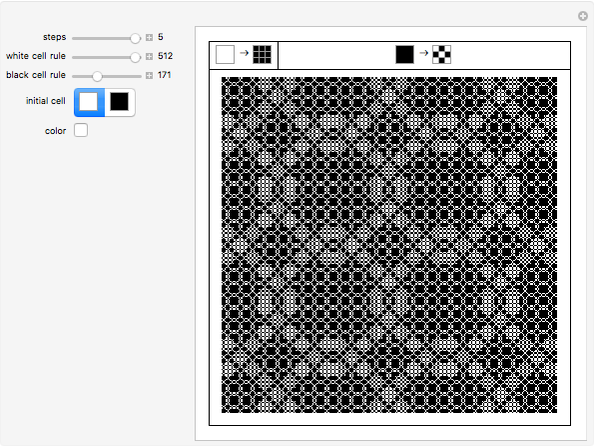
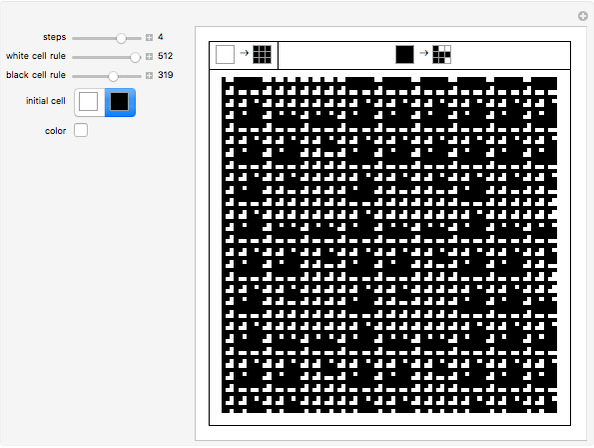
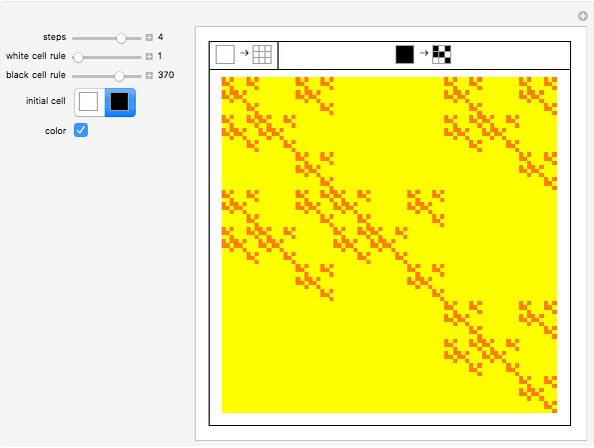
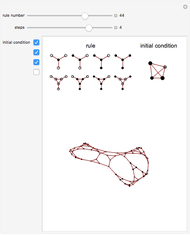
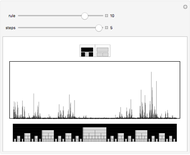
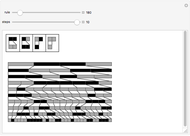
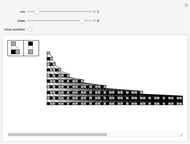
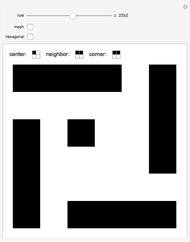
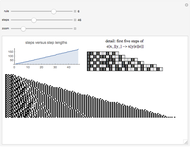
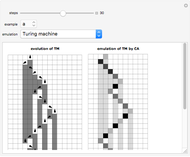
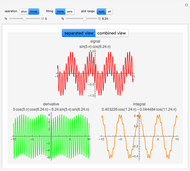
Interesting nested patterns can be found with a substitution system that splits each cell into nine cells at each step. There are 512 possible ways to split the white and black cells, for a total of 262144 possibilities. The initial condition can be a white or black cell, which doubles the possibilities.

This process gives a kind of fractal because the results show self-similarity. The Haferman carpet is one of the possible patterns.