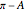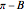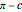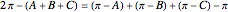Supplementary Solid Angles for Trihedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
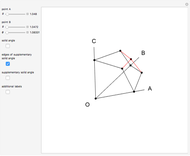
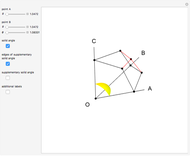
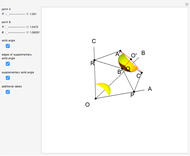
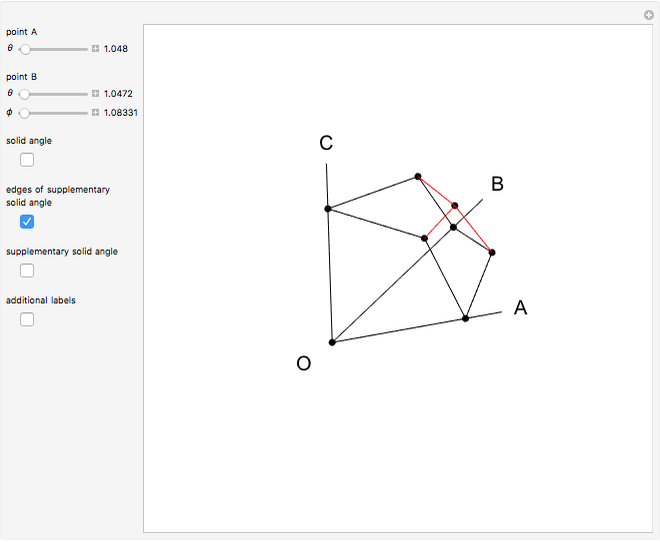
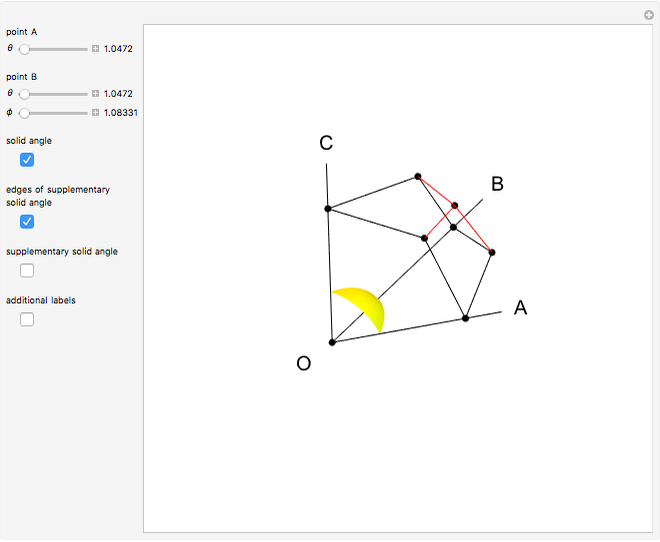
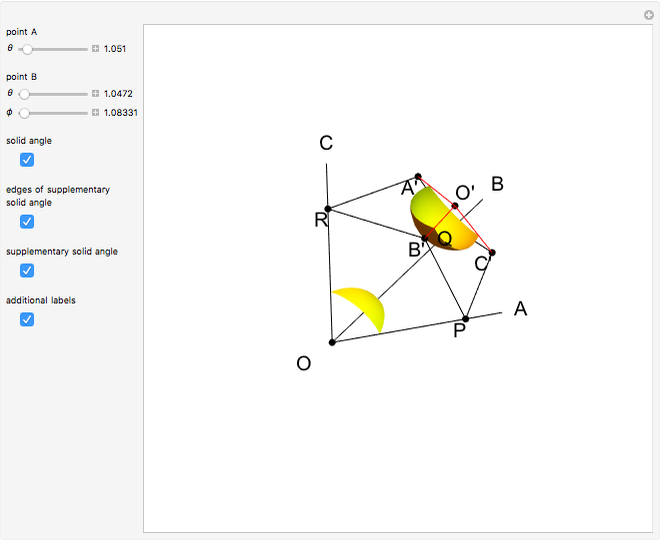
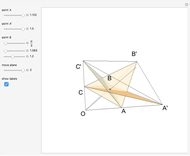
This Demonstration constructs a supplementary solid angle for a given trihedral solid angle. Let  ,
, 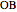 and
and 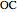 be the edges of a trihedron that determines the solid angle. The plane angles opposite the edges are denoted
be the edges of a trihedron that determines the solid angle. The plane angles opposite the edges are denoted  ,
,  ,
,  and the dihedral angles at the edges are denoted
and the dihedral angles at the edges are denoted 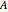 ,
, 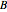 ,
, 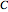 . Let
. Let 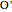 be a point inside the trihedron and denote its orthogonal projections onto the faces of the trihedron by
be a point inside the trihedron and denote its orthogonal projections onto the faces of the trihedron by 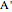 ,
,  and
and  . Then
. Then  ,
, 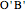 and
and 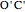 are edges of a trihedron that determines the supplementary space angle.
are edges of a trihedron that determines the supplementary space angle.
Contributed by: Izidor Hafner (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
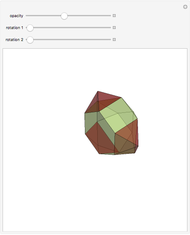
This Demonstration gives an animation for Figure 5.5 in [3, p. 186].
The deficiency of a solid angle determined by an  -sided spherical polygon with angles
-sided spherical polygon with angles 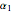 ,
, 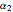 , …,
, …,  is
is  . The deficiency of a solid angle equals its supplementary angle [3, pp. 186–187].
. The deficiency of a solid angle equals its supplementary angle [3, pp. 186–187].
References
[1] Wikipedia. "Spherical Law of Cosines." (Feb 23, 2017) en.wikipedia.org/wiki/Spherical_law_of _cosines.
[2] Wikipedia. "Spherical Trigonometry." (Feb 23, 2017) en.wikipedia.org/wiki/Spherical_trigonometry.
[3] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997.
Permanent Citation