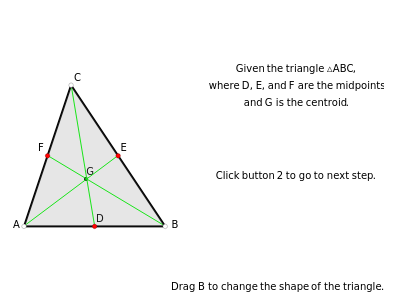
The Centroid of a Triangle Divides Each Median in the Ratio 1:2
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
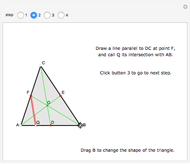
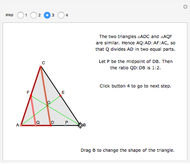
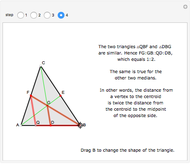
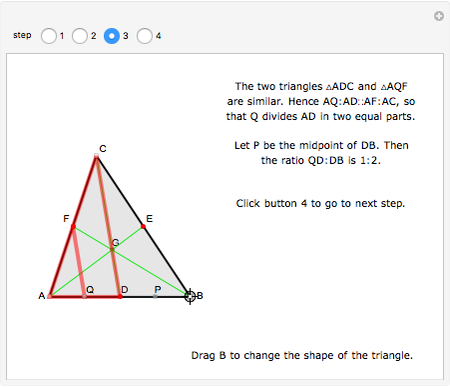
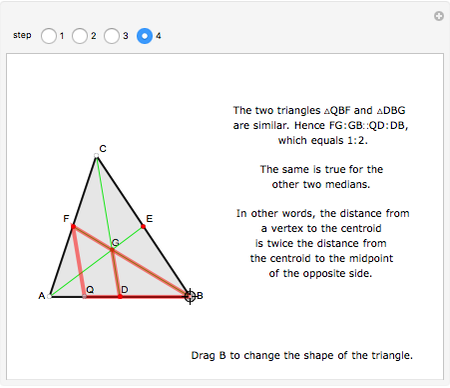
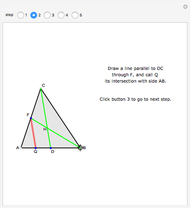
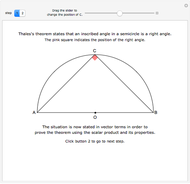
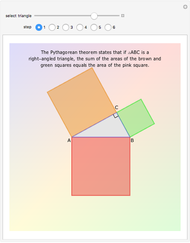
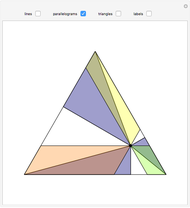
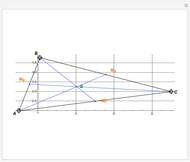
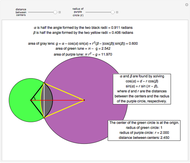
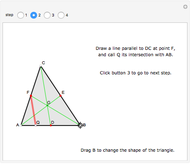
A median is the line from a midpoint of a side to the opposite vertex. The medians meet in the centroid, which is the center of mass of the triangle. A visual proof is given for the fact that the centroid of a triangle splits each of the medians in two segments, the one closer to the vertex being twice as long as the other one.
Contributed by: Tomas Garza (March 2011)
Open content licensed under CC BY-NC-SA