Monte Carlo Methods to Estimate Area

The area of the ellipse given by + =1 is estimated using three different Monte Carlo procedures.

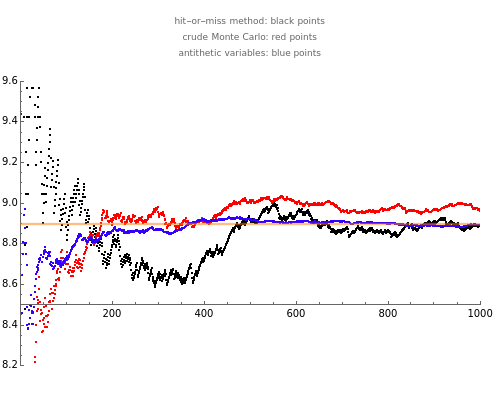
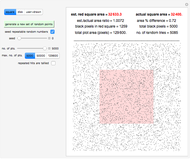
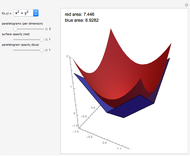
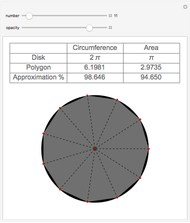
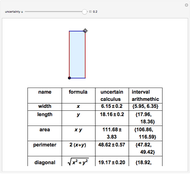
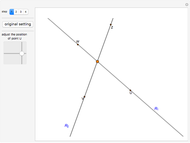
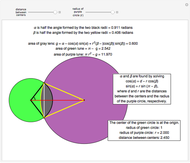
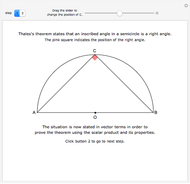
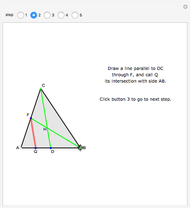
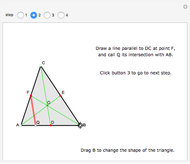
First, an ordinary hit-or-miss approach, which generates random points in the range , and then estimates the area as the proportion of those points that fall inside the ellipse multiplied by 8

Second, the procedure known as crude Monte Carlo, which looks at the integral giving the area beneath the curve as the expected value of some function, and then estimates it using the mean of that function evaluated at a number of random numbers with the corresponding probability distribution.

Thirdly, a refinement of the latter which uses antithetic random variables, that is, variables that are negatively correlated and which, adequately combined, produce an extremely good estimate.

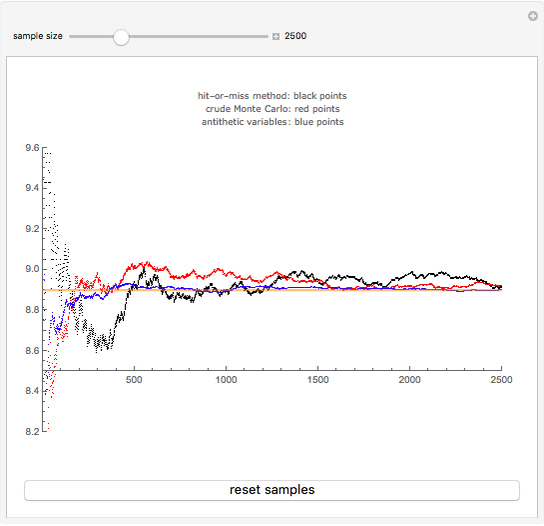
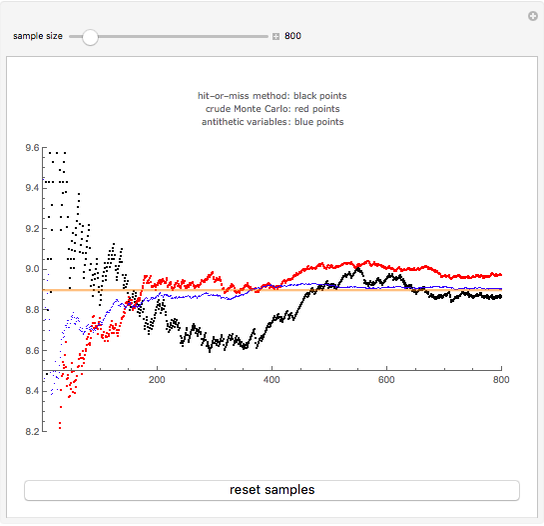
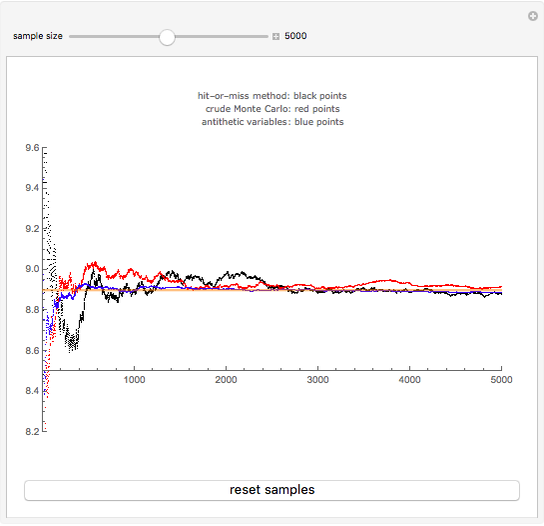
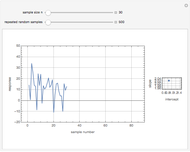
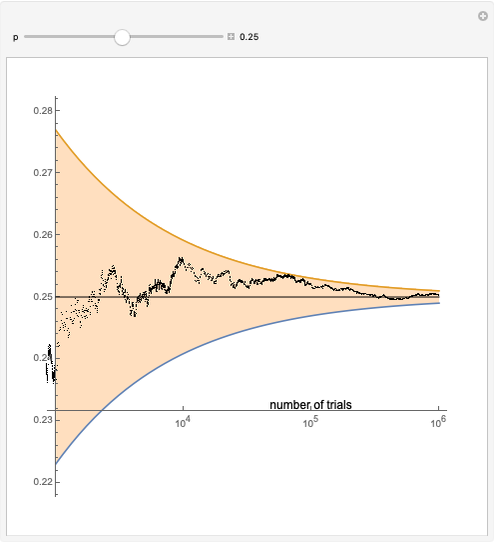
The behavior of the three approaches may be observed in the graph above. All of them provide an unbiased estimate of the area (equal to 8.89 in the example), but the antithetic variables method is seen to produce a more stable result as the sample size increases, while the other two exhibit a more fluctuating pattern.

Move the slider to see the effect of sample size on the estimation. Press the button to obtain a new set of random samples.