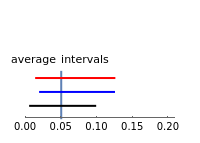
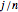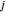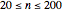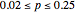Confidence Intervals, Confidence Levels, and Average Interval Length

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
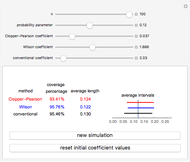
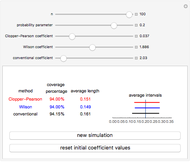
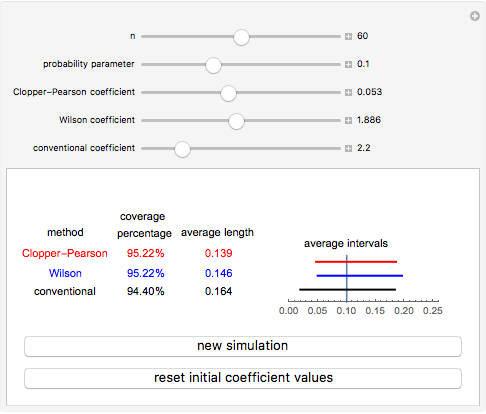
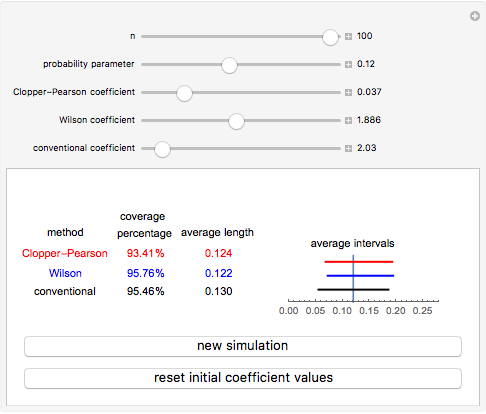
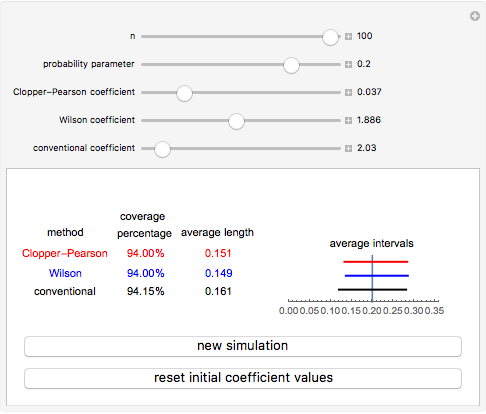
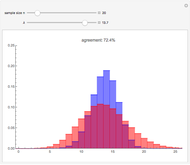
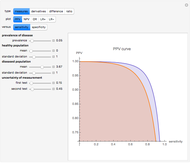
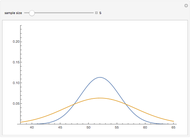
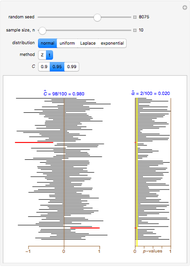
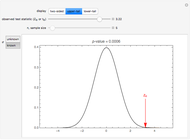
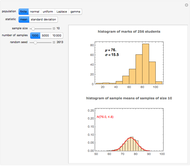
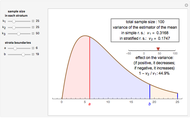
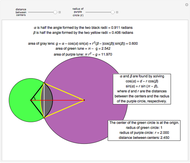
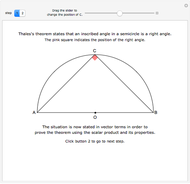
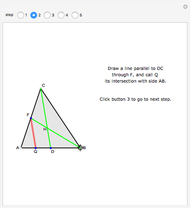
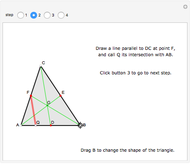
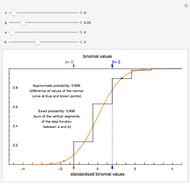
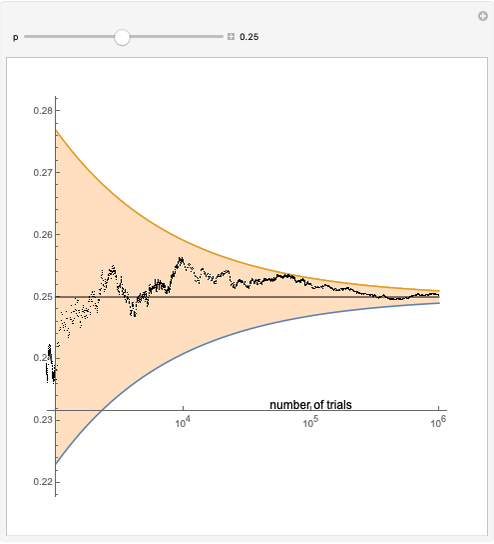
A confidence interval for estimating a parameter of a probability distribution must show two basic properties. First, it must contain the value of the parameter with a prescribed probability (the "confidence level"), and second, it must be as narrow as possible in order to be useful. Confidence intervals may be constructed in several ways, although in practice it is usually not possible to attain precisely the desired confidence level, contrary to common belief. This is illustrated in the present Demonstration for a binomial distribution with  trials and probability parameter
trials and probability parameter 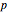 .
.
Contributed by: Tomas Garza (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The article on Binomial proportion confidence interval in Wikipedia gives the details for Wilson's method. Implementation of the Clopper–Pearson method is due to the author of this Demonstration.
Permanent Citation