The Completeness Theorem of Equivalential Calculus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
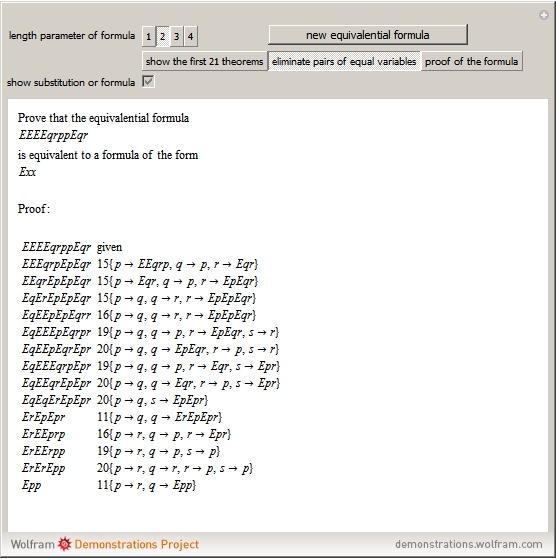
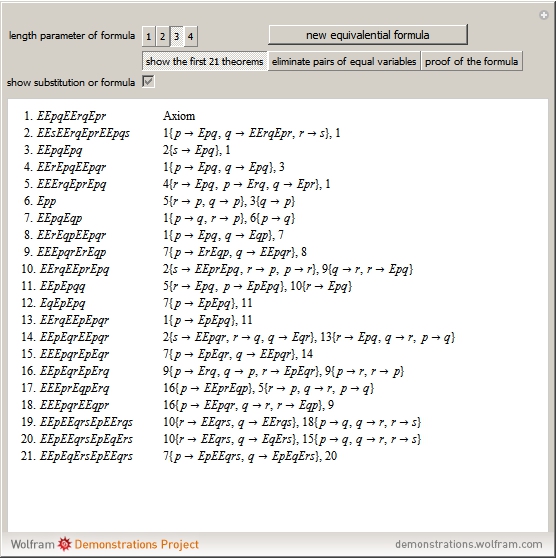
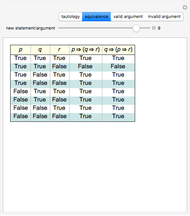
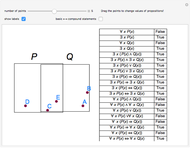
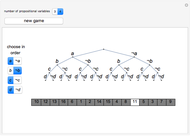
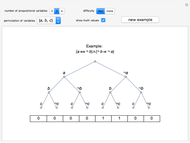
This Demonstration shows examples of Łukasiewicz's completeness theorem for the equivalential calculus. He first derived 21 theorems. Some of these theorems are associative and commutative rules on different parts of a formula. To show that a formula is a tautology, he eliminated pairs of the same propositional variable, to eventually get a formula of the form  . The proof of the formula
. The proof of the formula  goes in the opposite direction, and modus ponens is used in this form:
goes in the opposite direction, and modus ponens is used in this form:  follows from
follows from  and
and  . The first formula in the proof of
. The first formula in the proof of  is a substitution instance of theorem 6, that is, of
is a substitution instance of theorem 6, that is, of  . Each following formula follows by modus ponens from the one before it and from one of the 21 numbered theorems on which a substitution is applied.
. Each following formula follows by modus ponens from the one before it and from one of the 21 numbered theorems on which a substitution is applied.
Contributed by: Izidor Hafner (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
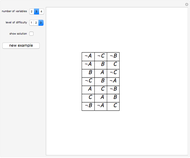
The equivalential calculus is a subsystem of propositional calculus with equivalence as the only connective. In 1929 Leśniewski recognized that the equivalential calculus could be axiomatized. He used two axioms and the rules of detachment and substitution. He also observed that a formula of propositional calculus in which equivalence was the only propositional function was a tautology if and only if each propositional letter occurs an even number of times. In 1932 Wajsberg showed that the calculus can be based on a single axiom. In 1933 Łukasiewicz found the shortest axiom,  , and gave a simple completeness proof. He first derived 21 tautologies. Some of them, such as
, and gave a simple completeness proof. He first derived 21 tautologies. Some of them, such as  , were used as rules. The rule
, were used as rules. The rule  says that a formula of the form
says that a formula of the form  is equivalent to
is equivalent to  . A formula of the calculus is a tautology if it is deductively equivalent to
. A formula of the calculus is a tautology if it is deductively equivalent to  , where
, where  is a propositional variable [1]. The realization of the completeness theorem as a Prolog program was given in [3].
is a propositional variable [1]. The realization of the completeness theorem as a Prolog program was given in [3].
In 1981 Hafner gave a more complicated completeness proof showing that the proof length (the number of proof steps) is linear in the formula size [2].
[1] J. Łukasiewicz, "The Equivalential Calculus," in Polish Logic (1920–1939), S. McCall, ed., Oxford: Clarendon Press, 1967 pp. 90–91.
[2] I. Hafner, "On Proof Length in the Equivalential Calculus," Glasnik Matematički, 15(35), 1980 pp. 233–242.
[3] I. Hafner, "The Completeness Theorem of Equivalential Calculus as Prolog Program," Logic Programming Newsletter, May 1987 pp. 7–8.
[4] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002 p. 1170e.
Permanent Citation