The Deltoid is a Kakeya Set

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
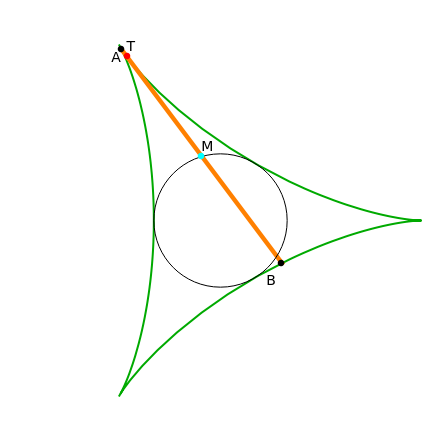
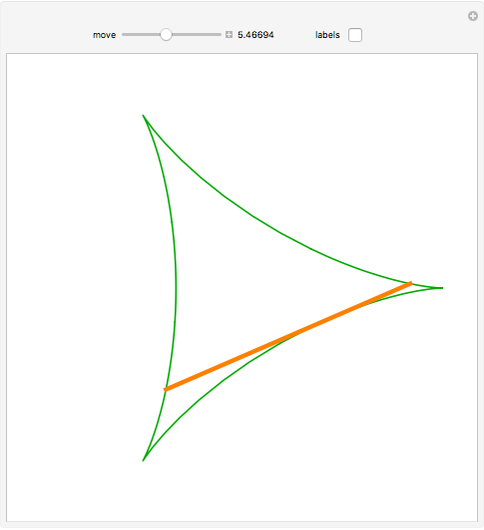
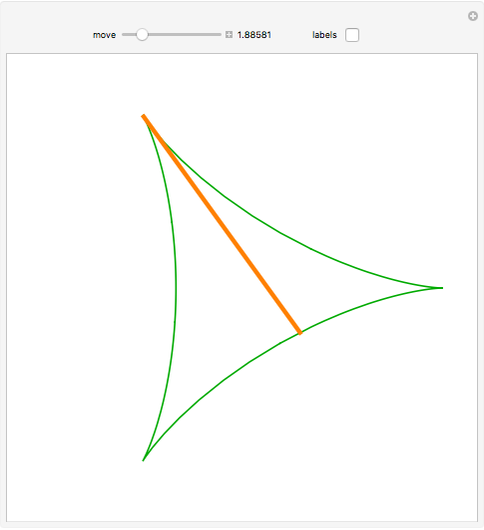
A circle  of radius 1 rolls inside a fixed circle of radius 3 (the fixed circle is shown when "labels" is selected); a point on the circumference of
of radius 1 rolls inside a fixed circle of radius 3 (the fixed circle is shown when "labels" is selected); a point on the circumference of  traces out the green curve, called a deltoid (or tricuspoid). Let the tangent to the deltoid at
traces out the green curve, called a deltoid (or tricuspoid). Let the tangent to the deltoid at  meet the deltoid again at
meet the deltoid again at  and
and  . Then the midpoint
. Then the midpoint  of
of  lies on the circle of radius 1 with center at origin. The length of
lies on the circle of radius 1 with center at origin. The length of  is 4, so the deltoid is a Kakeya set: a set through which a line segment can be moved back to itself but turned 180°.
is 4, so the deltoid is a Kakeya set: a set through which a line segment can be moved back to itself but turned 180°.
Contributed by: Izidor Hafner (June 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Kakeya needle problem asks whether there is a minimum area for a region  in the plane such that a needle of unit length can be turned through 180° [3].
in the plane such that a needle of unit length can be turned through 180° [3].
The deltoid is a hypocycloid of three cusps. It was first studied by Euler in 1745. The curve is also called a Steiner curve [4].
References
[1] D. G. Wells, The Penguin Dictionary of Curious and Interesting Geometry, New York: Penguin Books, 1991 p. 52 and p. 129.
[2] E. W. Weisstein. "Deltoid" from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/Deltoid.html (Wolfram MathWorld).
[3] Wikipedia. "Kakeya Set." (Jun 13, 2016) en.wikipedia.org/wiki/Kakeya_set.
[4] Wikipedia. "Deltoid Curve." (Jun 13, 2016) en.wikipedia.org/wiki/Deltoid_curve.
Permanent Citation