Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tracing a Peritrochoid

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

This Demonstration shows a mechanism drawing a peritrochoid.

[more]

Like the epitrochoid, a peritrochoid is the roulette traced by a point attached to a circle rolling without slipping around a base circle.

An epitrochoid is formed when the rolling circle is outside the base circle. A peritrochoid is formed when the base circle is inside the rolling circle.

While the traced epitrochoid and peritrochoid are similar, they are generated in different ways.

Peritrochoid curves appear in the kinematics of the Wankel engine [1].

[less]

Contributed by: Erik Mahieu (March 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

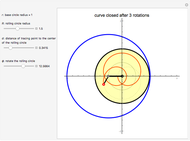
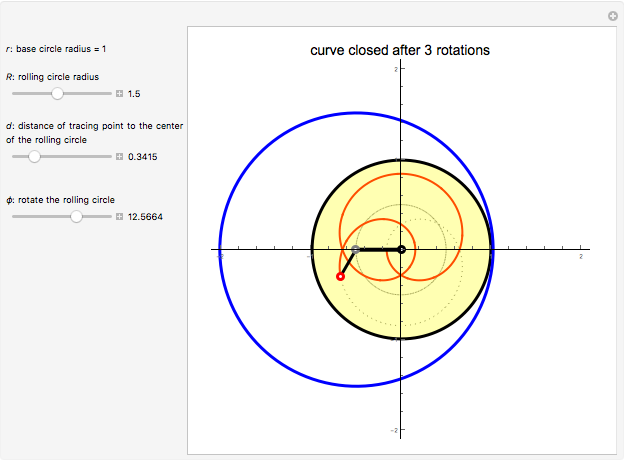
The radius of the stationary circle is set to 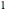, and 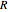is the radius of the rolling circle.

A peritrochoid is a sum of two rotations of the rolling circle, expressed in terms of their angle vectors:

1. A rotation around the axes origin: .

2. A rotation around its center: .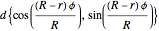

The peritrochoid becomes a closed curve after 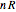rotations of the rolling circle, where is the denominator of a rational close to .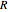

Reference

[1] V. I. Koutsovoulos. "Peritrochoid Curve & the Wankel Engine." Mechanical Drafting Services (Mar 6, 2017) mechdrafting.net/en/portfolio-item/peritrochoid-curve.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send