The Group of Rotations of the Cube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
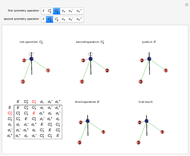
Consider a particular representation,  , of
, of 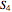 on
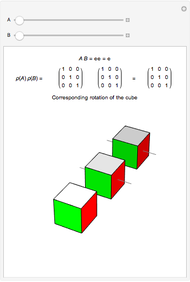
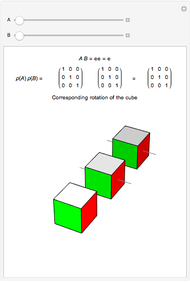
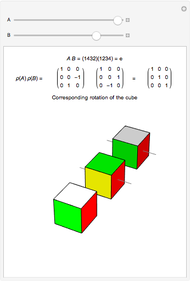
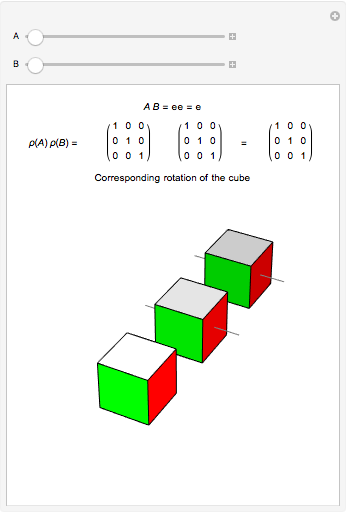
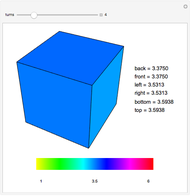
on 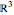 that preserves a cube centered at the origin, with faces orthogonal to the axes. By examining the action of elements of the group on the cube, both singly and in composition with other elements, you can see that
that preserves a cube centered at the origin, with faces orthogonal to the axes. By examining the action of elements of the group on the cube, both singly and in composition with other elements, you can see that 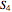 is isomorphic to the group of rotations of the cube. The brightest cube is fixed and the next two cubes show the actions of
is isomorphic to the group of rotations of the cube. The brightest cube is fixed and the next two cubes show the actions of 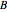 and
and 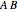 . The axes of rotation are shown in gray. The thickest axis represents
. The axes of rotation are shown in gray. The thickest axis represents 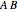 .
.
Contributed by: Keith Schneider (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
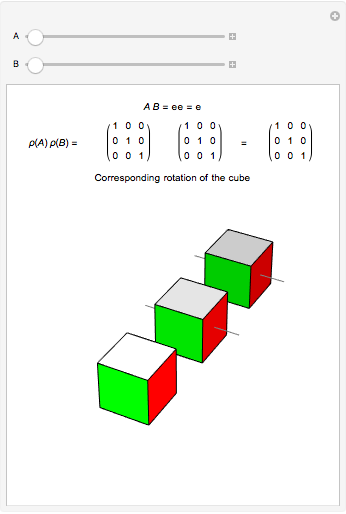
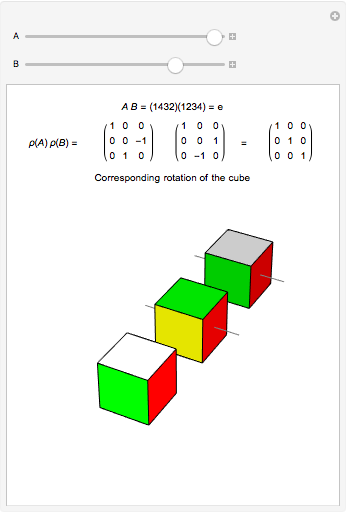
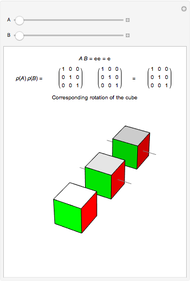
The two sliders can be used to select elements 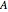 and
and 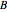 from
from 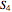 . These elements are shown in cycle form, as is their composition,
. These elements are shown in cycle form, as is their composition, 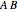 . Below that are the matrices of
. Below that are the matrices of 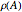 ,
,  , and
, and 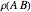 . The graphic shows how these matrices act on a cube centered at the origin, with faces orthogonal to the axes. The brightest cube is fixed, and displayed only as a point of reference. The middle cube (slightly darker) shows the action of
. The graphic shows how these matrices act on a cube centered at the origin, with faces orthogonal to the axes. The brightest cube is fixed, and displayed only as a point of reference. The middle cube (slightly darker) shows the action of 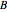 on the fixed cube, where the gray line shows the axis of rotation. The action of
on the fixed cube, where the gray line shows the axis of rotation. The action of 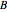 is first, since the operation throughout is composition. The third and darkest cube shows both the action of
is first, since the operation throughout is composition. The third and darkest cube shows both the action of 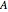 on the cube already acted on by
on the cube already acted on by 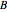 and the action of
and the action of 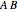 on the fixed cube. The thinner gray line shows the axis of rotation of
on the fixed cube. The thinner gray line shows the axis of rotation of 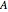 and the thicker gray line shows the the axis of rotation of the composition
and the thicker gray line shows the the axis of rotation of the composition 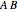 . By experimenting with different elements and compositions of elements, you can verify that
. By experimenting with different elements and compositions of elements, you can verify that  is isomorphic to the group of rotations of the cube.
is isomorphic to the group of rotations of the cube.
Permanent Citation