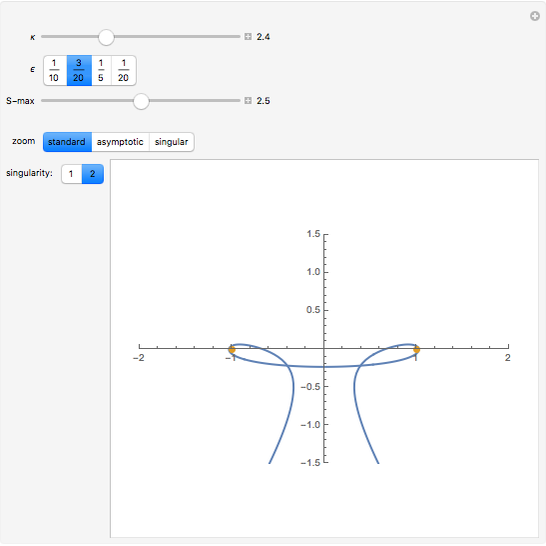
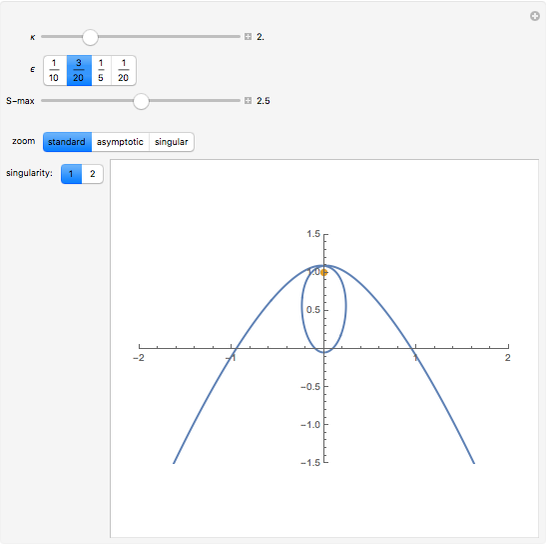
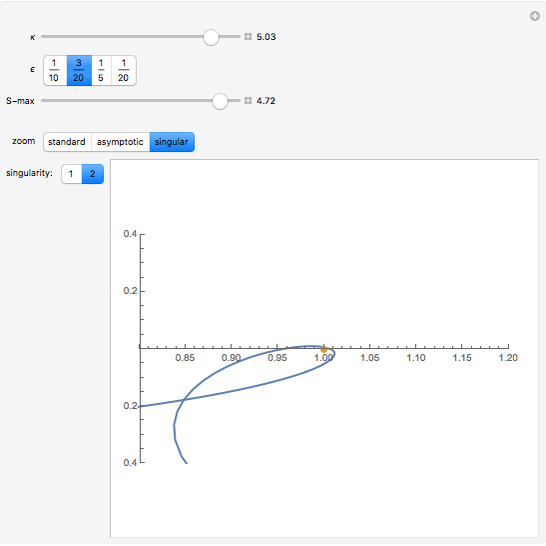
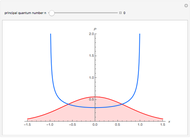
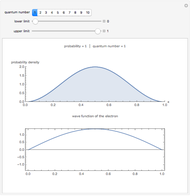
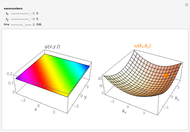
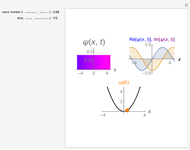
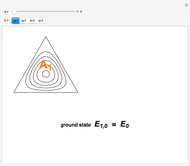
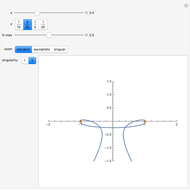
The PT-symmetric quantum mechanics is a generalization of the classical quantum mechanics where Hamiltonians are not necessarily Hermitian. This Demonstration provides intuition for quantum-tobogganic paths. They represent an extension of the usual real coordinates into the complex plane, which just trade off the dynamics generated by the potential and the dynamics generated by the topology. The PT-symmetric quantum-tobogganic paths have to be left-right symmetric (to ensure the spectrum is real) and their initial and final parts do not need to be on the same Riemann sheet. The current case presents the tobogganic paths (a conformal mapping) for the case of one and two branch points.