Quantum Particles in an Infinite Square Potential Well

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
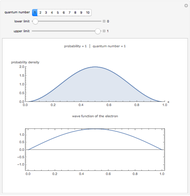
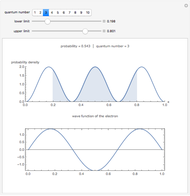
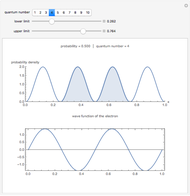
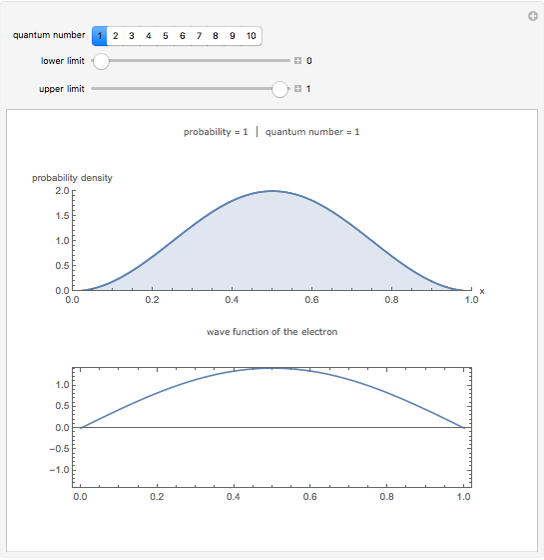
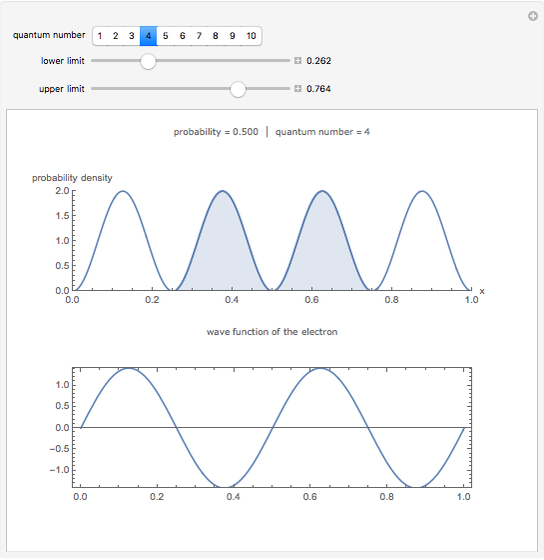
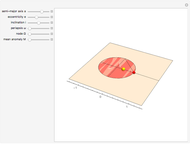
This Demonstration shows the probability of finding an electron in an infinite square potential well (top graphic) and also shows the wave function of the electron (bottom graphic).
Contributed by: Jeff Bryant (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
quantum number — an integer value, one of the discrete quantum states of the electron
lower and upper limits — the lowest and highest x values for the position of the electron
The one-dimensional solution to Schrödinger's equation for an electron in an infinite square potential well (normalized to be of width 1) is  , where
, where  is the quantum number. The square of this wave function is the probability density function for the electron.
is the quantum number. The square of this wave function is the probability density function for the electron.
The probability of finding the electron somewhere inside the square well is 1. (snapshot 1)
The probability of finding the electron with a quantum number of 3 between 0.2 and 0.8 is approximately 0.54. (snapshot 2)
The probability of finding the electron with a quantum number of 4 between 0.25 and 0.75 is approximately 0.5. (snapshot 3)
Permanent Citation
"Quantum Particles in an Infinite Square Potential Well"
http://demonstrations.wolfram.com/QuantumParticlesInAnInfiniteSquarePotentialWell/
Wolfram Demonstrations Project
Published: March 7 2011