Addition of Angular Momenta in Quantum Mechanics

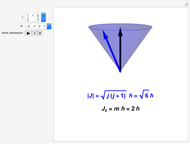
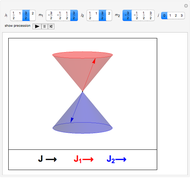
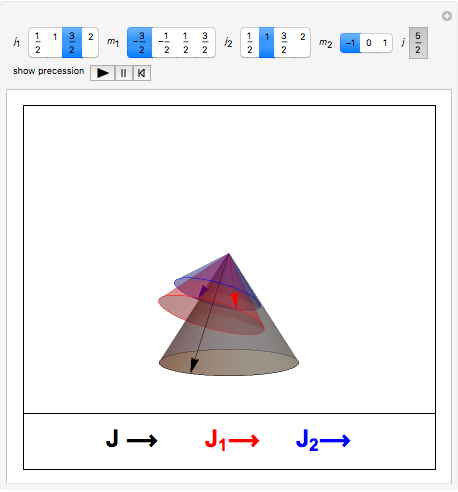
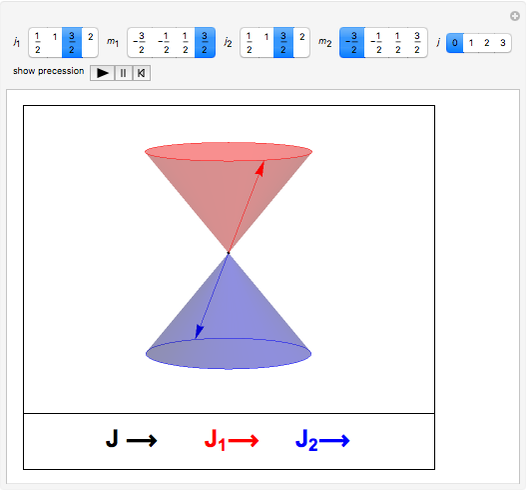
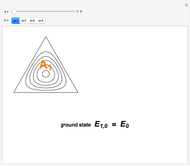
Angular momentum in quantum mechanics is a quantized vector with magnitude and component in any direction, conventionally chosen as the axis. The quantum numbers are restricted to integer or half-integer values: , with . Vector addition of two angular momenta is restricted by a triangle inequality with . Although quantum formalism is indifferent to such interpretations, the addition of angular momentum in the absence of any electric or magnetic field can be pictured by a vector model in which and precess about , which itself precesses about a axis. The amplitude for addition of and to give with component can be expressed in terms of Clebsch–Gordan coefficients as with the sum restricted by . You can set the precessions into motion with the trigger control. To choose a new set of and values, pause and reset the trigger.