Torricelli's Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Torricelli's theorem states that the velocity of efflux for a nonviscous fluid flowing from a cylindrical tank is  where
where  is the acceleration due to gravity (10
is the acceleration due to gravity (10  ) and
) and  is the distance between the surface of the water and the location of the spigot. However, this does not specify the exact coefficient because it assumes that the velocity of the water at the surface of the tank is negligible and that both the tank and the spigot are exposed to atmospheric pressure. If the velocity of the water at the surface is taken into account, the formula for the velocity of efflux becomes
is the distance between the surface of the water and the location of the spigot. However, this does not specify the exact coefficient because it assumes that the velocity of the water at the surface of the tank is negligible and that both the tank and the spigot are exposed to atmospheric pressure. If the velocity of the water at the surface is taken into account, the formula for the velocity of efflux becomes 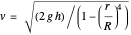 , where it takes into account
, where it takes into account  , the radius of the spigot, and
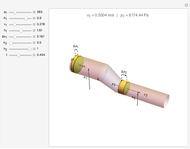
, the radius of the spigot, and 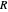 , the radius of the cylindrical tank. This equation can be derived from Bernoulli's equation,
, the radius of the cylindrical tank. This equation can be derived from Bernoulli's equation,  , and the continuity equation,
, and the continuity equation, 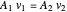 .
.
Contributed by: Ernest Lee (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
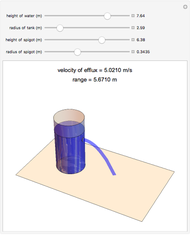
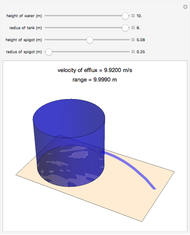
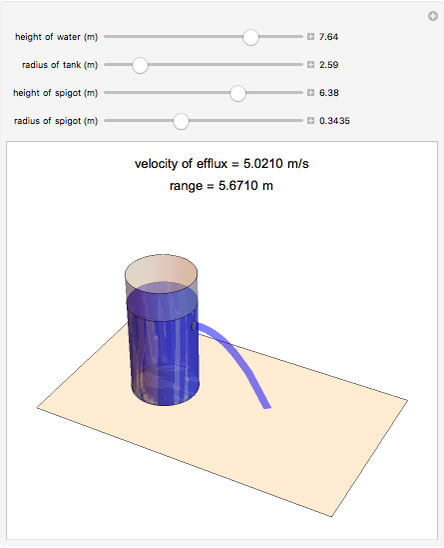
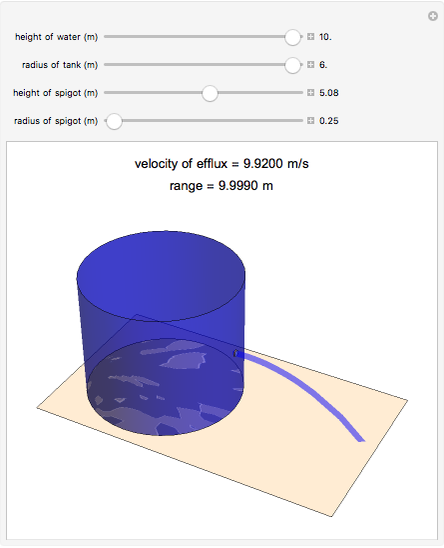
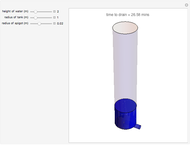
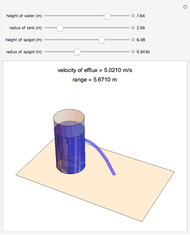
The height of the water, radius of the tank, location of the spigot, and the radius of the spigot can be changed by moving the sliders. The velocity of efflux and the range of the emptying water change as different parameters of the tank are modified. The 3D graphics reflect the dimensions of the cylindrical tank and the path of the water out of the spigot.
Permanent Citation