Inviscid Burgers's Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
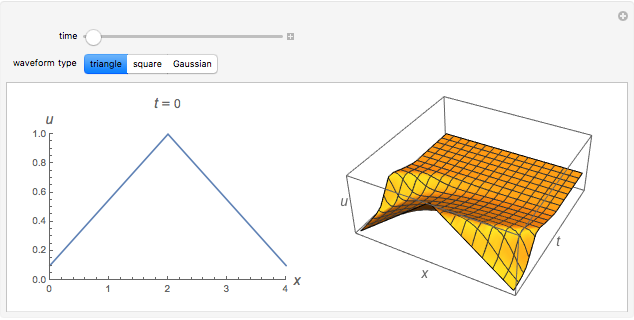
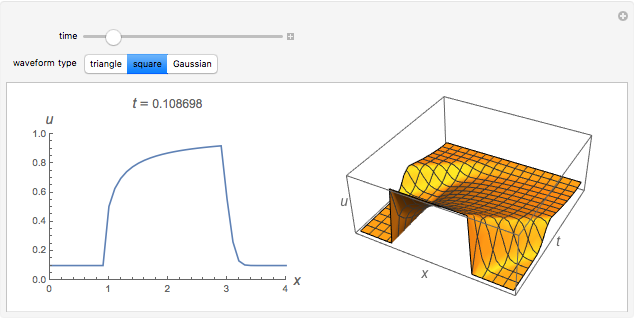
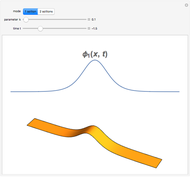
Burgers's equation is one of the simplest cases of a nonlinear, hyperbolic partial differential equation. It is useful as a test problem in computational fluid dynamics. The one-dimensional, inviscid (i.e., zero viscosity) form of the equation is given by
[more]
Contributed by: Garrett Neske (March 2011)
Open content licensed under CC BY-NC-SA
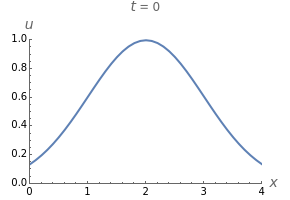
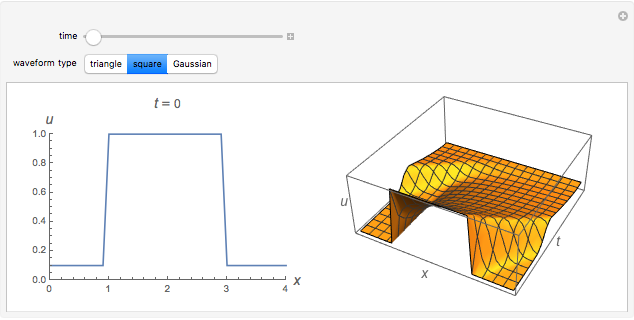
Snapshots
Details
The inviscid Burgers's equation is a flux-conservative partial differential equation, and is thus amenable to finite-volume methods, which are often used for numerically solving nonlinear, hyperbolic partial differential equations. Hyperbolic problems are represented in the flux-conserving form
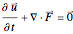 ,
,
where 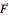 is the flux function for some conserved quantity
is the flux function for some conserved quantity  . The inviscid Burgers's equation is easily represented in this form if the flux function is considered to be
. The inviscid Burgers's equation is easily represented in this form if the flux function is considered to be 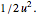 The finite-volume method takes the following form with forward-Euler time-stepping
The finite-volume method takes the following form with forward-Euler time-stepping
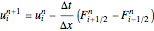 ,
,
where  is the space index,
is the space index,  is the time index,
is the time index, 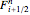 is the flux at the right boundary enclosing the volume around point
is the flux at the right boundary enclosing the volume around point  , and
, and 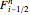 is the flux at the left boundary enclosing the volume around point
is the flux at the left boundary enclosing the volume around point  . There are several different finite-volume methods, which differ in their determination of
. There are several different finite-volume methods, which differ in their determination of 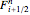 and
and 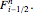 In this Demonstration, the Harten-Lax-van Leer (HLL) method is used because it is good at capturing shocks in an evolving waveform, which is a feature often found in solutions to Burgers's equation.
In this Demonstration, the Harten-Lax-van Leer (HLL) method is used because it is good at capturing shocks in an evolving waveform, which is a feature often found in solutions to Burgers's equation.
Reference: R. J. LeVeque, Finite Volume Methods for Hyperbolic Problems, Cambridge, UK: Cambridge University Press, 2002.
Permanent Citation