Logarithmic Spirals and Möbius Transformations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
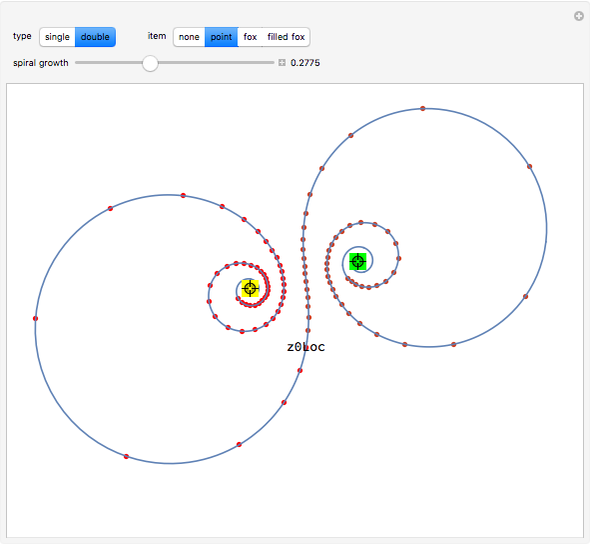
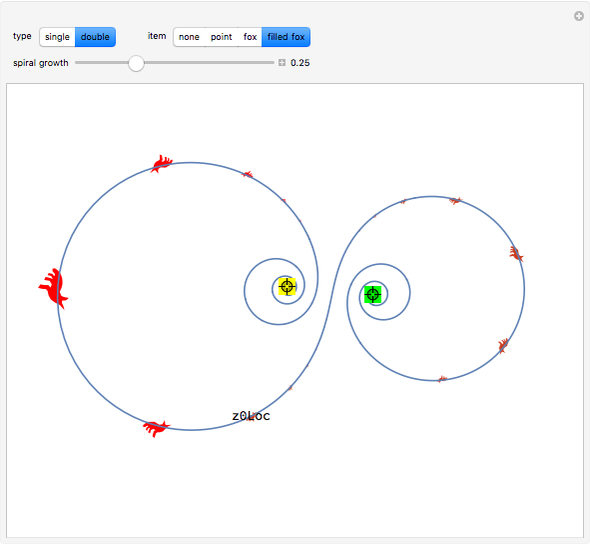
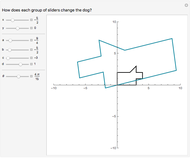
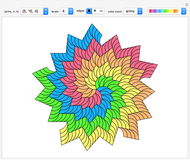
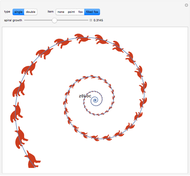
You can vary the parameters of the logarithmic spiral pictured here, and convert it to a double spiral by an appropriate Möbius transformation. You can then drag the centers of the spirals with locators.
Contributed by: Dieter Steemann (February 2017)
Open content licensed under CC BY-NC-SA
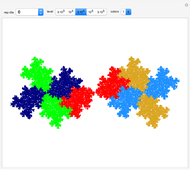
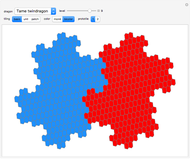
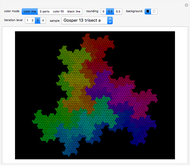
Snapshots
Details
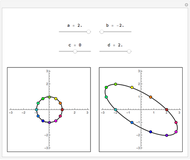
A logarithmic spiral can be parametrized by  , where
, where  is the point in the complex plane corresponding to
is the point in the complex plane corresponding to  . The complex parameter
. The complex parameter  determines the spiral's rate of growth. When
determines the spiral's rate of growth. When  , the spiral curls outward with increasing positive
, the spiral curls outward with increasing positive  and tends to infinity. Increasing negative values of
and tends to infinity. Increasing negative values of  make the spiral curl inward toward the origin. You can vary the spiral growth (curling)
make the spiral curl inward toward the origin. You can vary the spiral growth (curling)  with the "spiral growth" slider.
with the "spiral growth" slider.
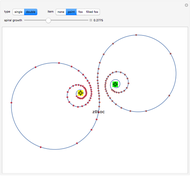
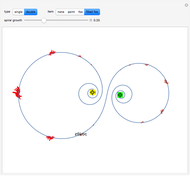
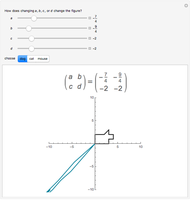
In this Demonstration, such a spiral is shown by selecting the type "single". You can change  by dragging the magenta locator in the graphic. When the type "double" is selected, the spiral is mapped into a double spiral by a specific Möbius transformation. Then you can vary two additional parameters. The yellow locator determines the source location of the Möbius transformation, and the green one the sink location.
by dragging the magenta locator in the graphic. When the type "double" is selected, the spiral is mapped into a double spiral by a specific Möbius transformation. Then you can vary two additional parameters. The yellow locator determines the source location of the Möbius transformation, and the green one the sink location.
The Möbius transformation (or linear fractional transformation)  moves a point at the origin of the complex plane to
moves a point at the origin of the complex plane to  (the source) and a point at
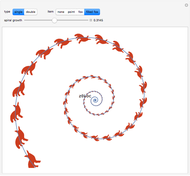
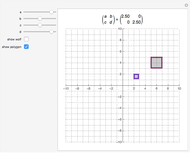
(the source) and a point at  to 1 (the sink) in the complex plane. Here, a more flexible transformation is used, in which the locations of both source and sink can be set. The action of this transformation can be seen when the graphic figure "fox" is selected for visualization. There exist exceptional parameter configurations in which a single "filled fox" covers the entire graphic. Keep changing the parameter or select the "unfilled" fox in such a situation.
to 1 (the sink) in the complex plane. Here, a more flexible transformation is used, in which the locations of both source and sink can be set. The action of this transformation can be seen when the graphic figure "fox" is selected for visualization. There exist exceptional parameter configurations in which a single "filled fox" covers the entire graphic. Keep changing the parameter or select the "unfilled" fox in such a situation.
This Demonstration is inspired by [1] and the corresponding Fortran program "kleinian" [2].
References
[1] D. Mumford, C. Series and D. Wright, Indra's Pearls: The Vision of Felix Klein, Cambridge: Cambridge University Press, 2006 pp. 62.
[2] D. J. Wright, "Limit Sets of Kleinian Groups." (Feb 8, 2017) klein.math.okstate.edu/IndrasPearls/limitsets.
Permanent Citation