Trajectory of a Particle around Two Black Holes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
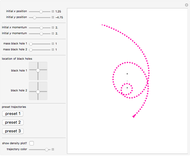
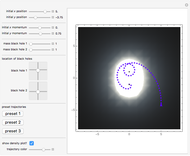
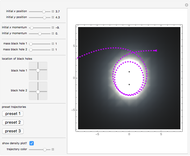
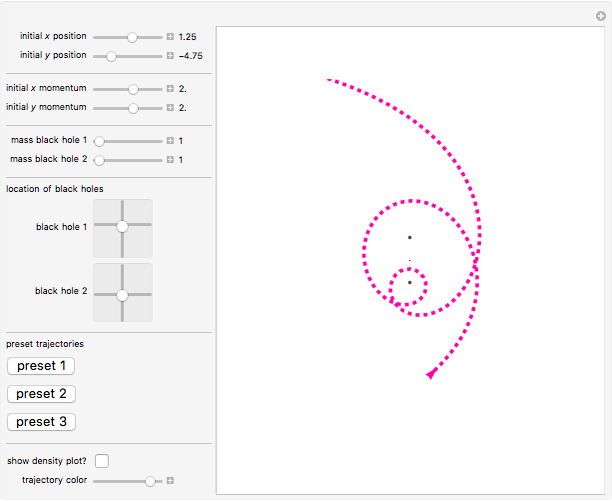
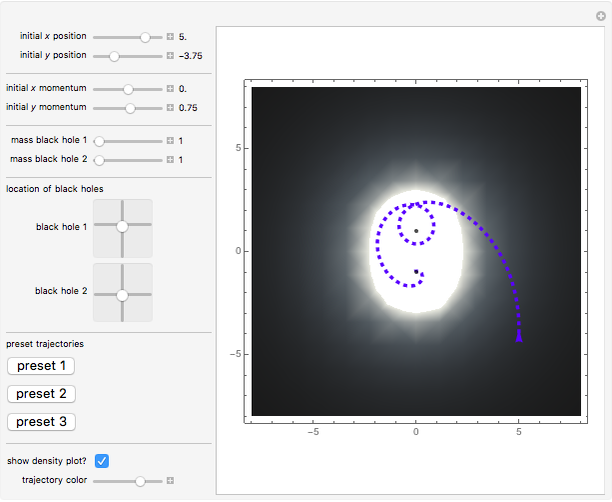
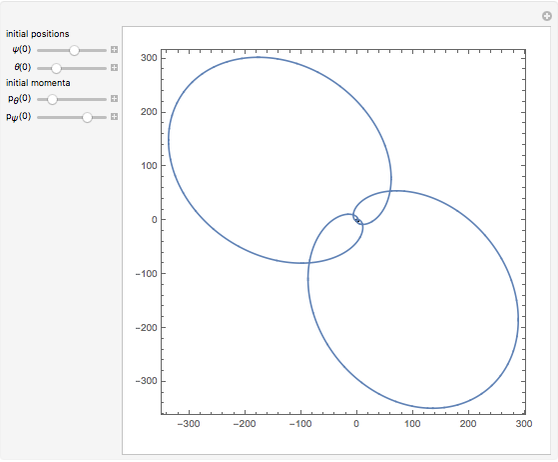
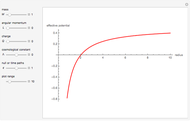
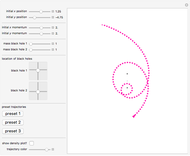
This Demonstration shows some possible trajectories of a particle as it passes near two black holes. The trajectory of the particle depends on its initial position and initial momentum, as well as the mass of each black hole and their locations. These initial conditions determine whether the particle orbits around the black holes and escapes or whether it is captured by one of them. The density plot represents the effective potential energy of the black holes.
Contributed by: Nora Finegan and Jiamin Huang (June 2016)
Special thanks to the University of Illinois NetMath Program and the mathematics department at William Fremd High School.
After work by: Jason Cole
With additional contributions by: Mr. Grattoni
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Majumdar–Papapetrou metric describes the path a particle takes near multiple black holes. The metric is given by  , where
, where 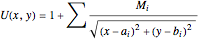 [1]. From this metric, we can find the equations for the derivative of the particle's momentum
[1]. From this metric, we can find the equations for the derivative of the particle's momentum  and position
and position  with respect to time in two dimensions [2]:
with respect to time in two dimensions [2]:
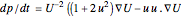 ),
),
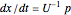 .
.
Snapshot 1: the trajectory of a particle with initial position 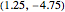 , initial momentum
, initial momentum 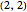 , with black holes of mass 1 and 1, and hue .89
, with black holes of mass 1 and 1, and hue .89
Snapshot 2: the trajectory of a particle with initial position 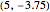 , initial momentum
, initial momentum 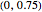 , with black holes of mass 1 and 1, with the density plot on, and hue of .725
, with black holes of mass 1 and 1, with the density plot on, and hue of .725
Snapshot 3: the trajectory of a particle with initial position 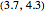 , initial momentum
, initial momentum  , with black holes of mass 1 and 1, with the density plot on, and hue of .795
, with black holes of mass 1 and 1, with the density plot on, and hue of .795
References
[1] J. Cole. "Black Holes and Fractal Basins." (Jun 8, 2016) jasmcole.com/2014/09/04/black-holes-and-fractal-basins.
[2] C. P. Dettmann, N. E. Frankel, and N. J. Cornish, "Chaos and Fractals Around Black Holes," Fractals, 3(1), 1995 pp. 161–181. doi:10.1142/S0218348X9500014X.
Permanent Citation