Effective and Inertial Masses of a Photon Near a Black Hole for a Family of Envelope Orbits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
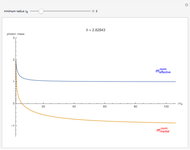
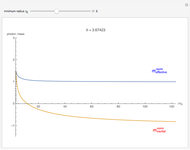
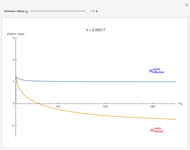
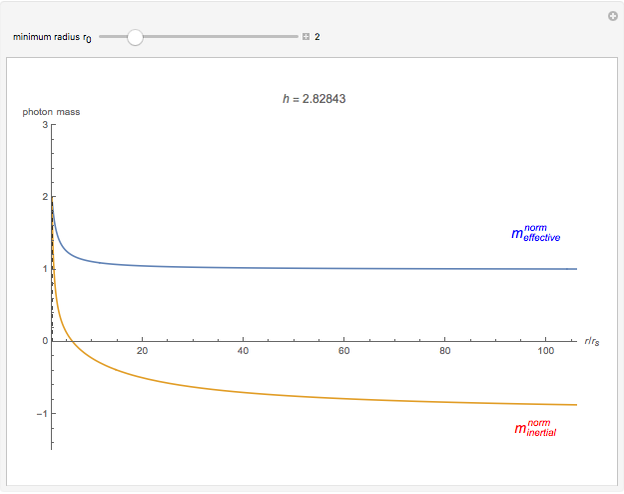
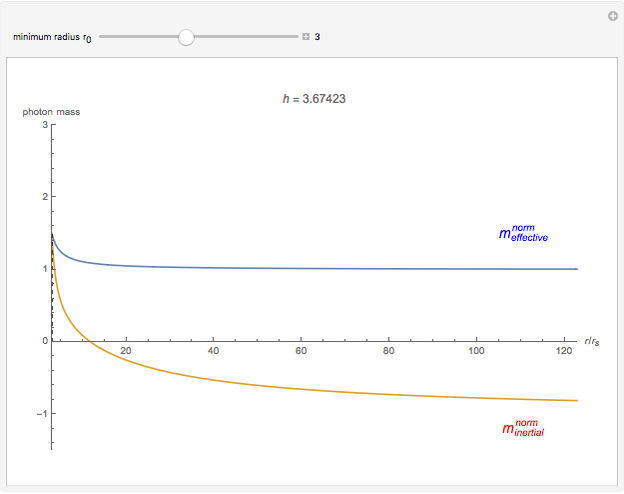
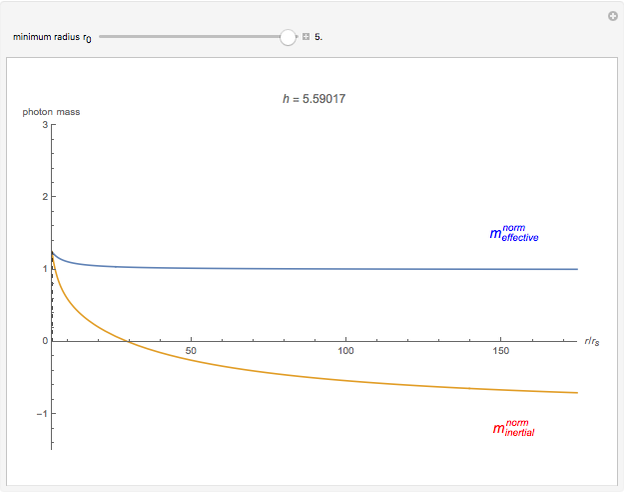
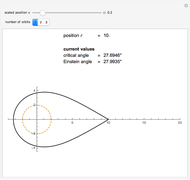
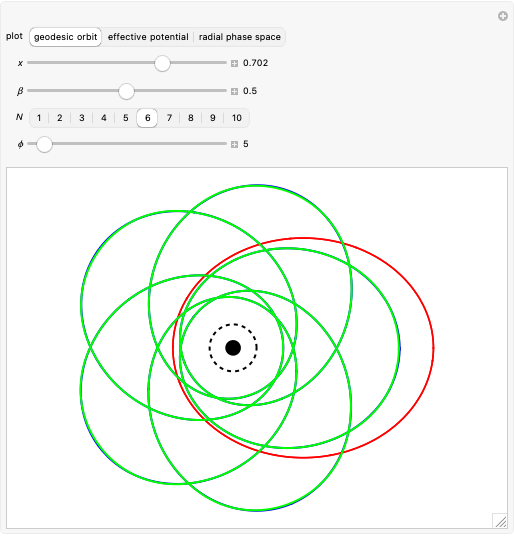
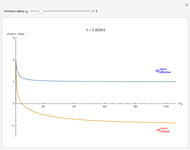
Photons move along geodesic paths, which are bent in a gravitational field. This allows one to assume that the photon has a finite inertial mass. This Demonstration shows how the effective and inertial masses change as functions of the distance  to the center of gravity and the motion constant
to the center of gravity and the motion constant  for the photon's orbits near a black hole with minimum radius
for the photon's orbits near a black hole with minimum radius 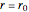 . The unit of distance is chosen as the Schwarzschild radius, such that
. The unit of distance is chosen as the Schwarzschild radius, such that  .
.
Contributed by: Wladimir Belayev (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The normalized effective mass of a photon can be defined by the proportionality between the canonical momentum  and the four-velocity
and the four-velocity  , such that
, such that  . In a central gravitational field, the normalized inertial mass is found from
. In a central gravitational field, the normalized inertial mass is found from  , where
, where 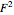 is the radial component of the canonical force vector. The relation between
is the radial component of the canonical force vector. The relation between  and
and  is obtained from the condition
is obtained from the condition  , leading to the constant of motion
, leading to the constant of motion  .
.
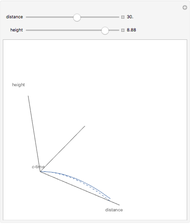
The decrease of the coordinate velocity in most of its trajectory in the gravitational field is known as the Shapiro time-delay effect. It can be pictured as a negative inertial mass for the photon. By contrast, a positive mass particle accelerates as it approaches the center of gravity.
For further technical details, please refer to W. Belayev, "Application of Lagrange Mechanics for Analysis of the Light-Like Particle Motion in Pseudo-Riemann Space," 2009, http://arxiv.org/abs/0911.0614.
Permanent Citation