Trinoids with Constant Mean Curvature

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
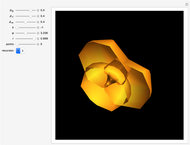
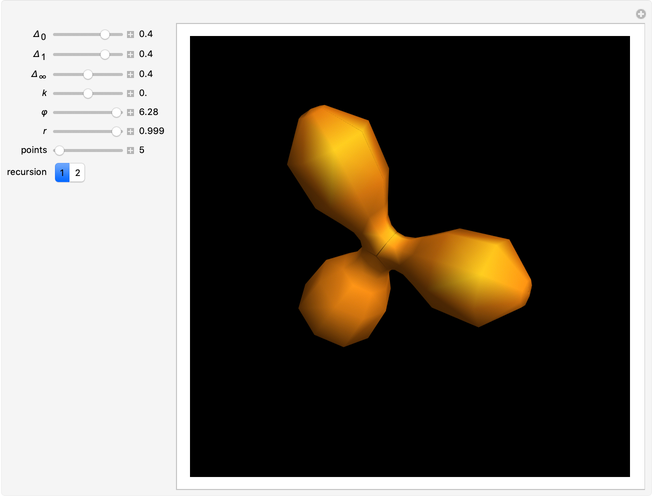
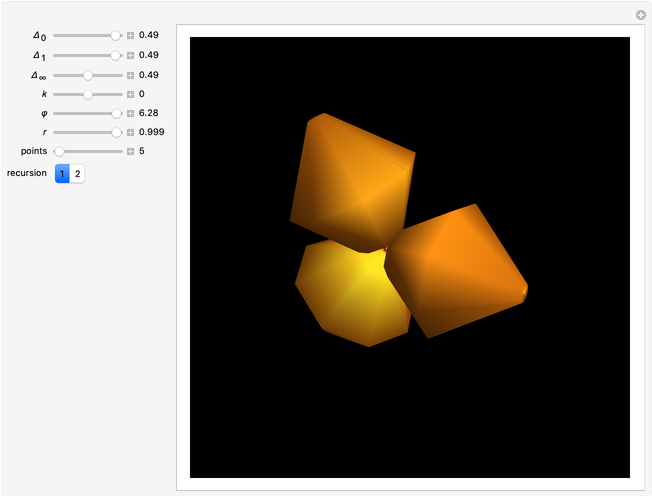
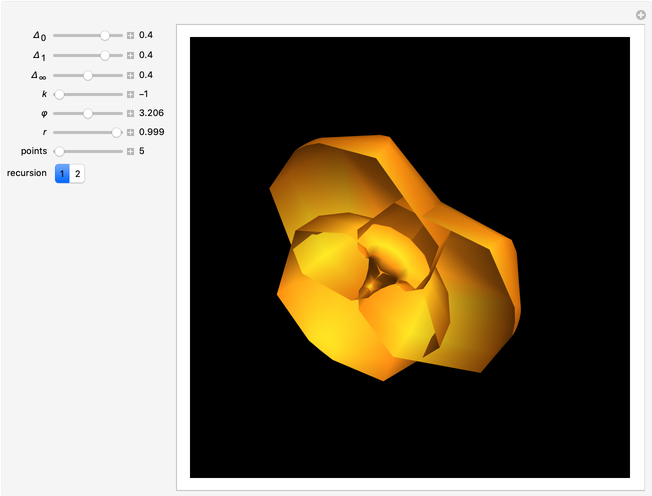
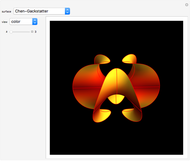
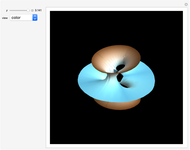
Trinoids with constant mean curvature are a family of surfaces that depend on the parameters  , related to the monodromy group. When
, related to the monodromy group. When  , the trinoid is symmetric [1]. The trinoid is embedded when
, the trinoid is symmetric [1]. The trinoid is embedded when  and the parameter
and the parameter  is related to the embeddedness. The equations are derived from Bryant holomorphic representation (analogous to the Weierstrass representation of minimal surfaces), in terms of gamma and hypergeometric functions.
is related to the embeddedness. The equations are derived from Bryant holomorphic representation (analogous to the Weierstrass representation of minimal surfaces), in terms of gamma and hypergeometric functions.
Contributed by: Enrique Zeleny (August 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
To be closed, the trinoids must simultaneously satisfy the following conditions:

Reference
[1] A. I. Bobenko, T. V. Pavlyukevich, and B. A. Springborn, "Hyperbolic Constant Mean Curvature One Surfaces: Spinor Representation and Trinoids in Hypergeometric Functions." lanl.arxiv.org/abs/math/0206021v2.
Permanent Citation