Trisection by Sliding a Line

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
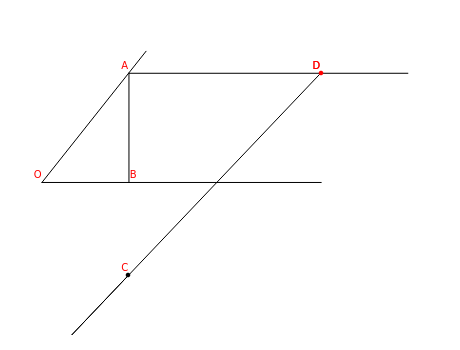
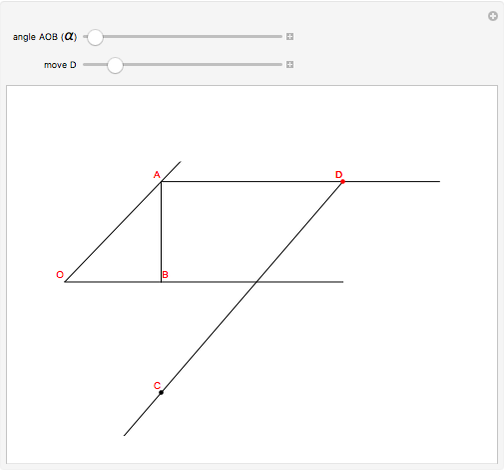
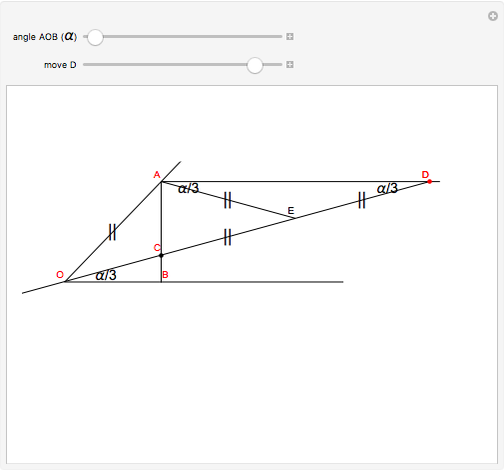
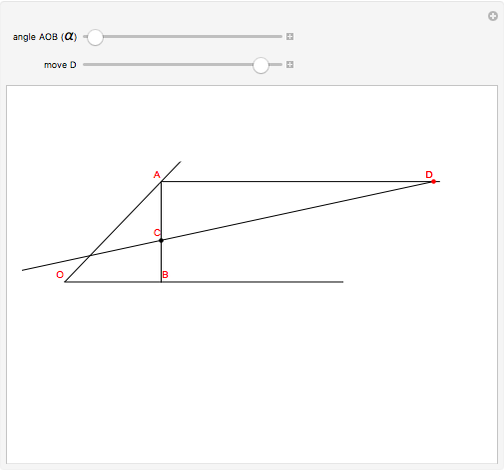
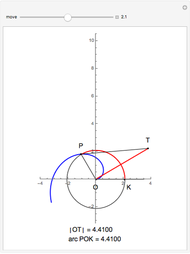
This Demonstration shows how to trisect an angle by sliding a line. Adjust the angle to trisect,  , and then move point
, and then move point  so that the point
so that the point  is on the line
is on the line  . The point
. The point  is chosen so that
is chosen so that  is twice
is twice  . The angle
. The angle  is a third of the angle
is a third of the angle  .
.
Contributed by: Izidor Hafner (July 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let  . Assume the line
. Assume the line  is parallel to
is parallel to  ,
,  is perpendicular to
is perpendicular to  , and
, and  . If the point
. If the point  is on the line
is on the line  , and
, and  , then triangles
, then triangles  and
and  are isosceles. The angles
are isosceles. The angles  and
and  are equal and are equal to
are equal and are equal to  , but their sum equals
, but their sum equals  . So
. So  .
.
The problem goes back to ancient Greece, with contributions by Hippocrates, Archimedes, and Pappus.
References
[1] P. Berloquin, The Garden of the Sphinx, New York: Scribner's, 1985 p. 179.
[2] J. J. O'Connor and E. F. Robertson. "Trisecting an Angle." (Jun 21, 2012) www-history.mcs.st-and.ac.uk/HistTopics/Trisecting_an_angle.html.
Permanent Citation