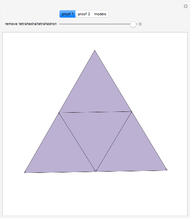
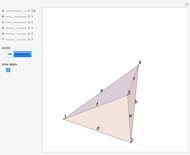
Volume of the Regular Tetrahedron and Regular Octahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
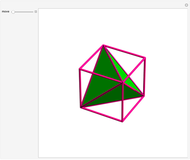
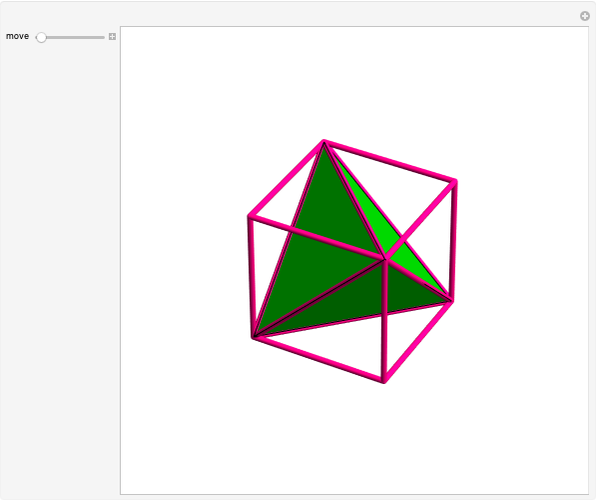
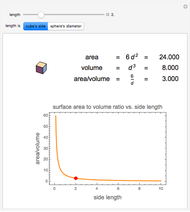
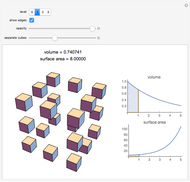
Let  be the length of an edge of a regular tetrahedron
be the length of an edge of a regular tetrahedron 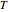 inscribed in a cube
inscribed in a cube 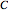 of edge length
of edge length 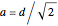 . Let
. Let 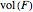 stand for the volume of a solid
stand for the volume of a solid 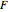 . We get
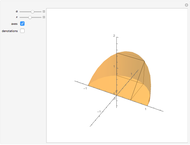
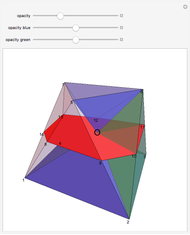
. We get 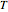 by cutting away four triangular pyramids from
by cutting away four triangular pyramids from 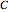 . The volume of such a pyramid
. The volume of such a pyramid 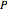 is
is 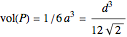 . Then
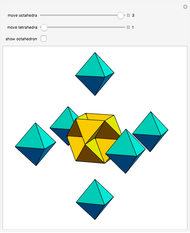
. Then 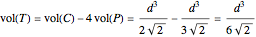 . But these four pyramids form one half of the regular octahedron
. But these four pyramids form one half of the regular octahedron  , which therefore has volume
, which therefore has volume 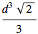 and the ratio
and the ratio 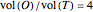 .
.
Contributed by: Izidor Hafner (November 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Volume of the Regular Tetrahedron and Regular Octahedron"
http://demonstrations.wolfram.com/VolumeOfTheRegularTetrahedronAndRegularOctahedron/
Wolfram Demonstrations Project
Published: November 13 2014