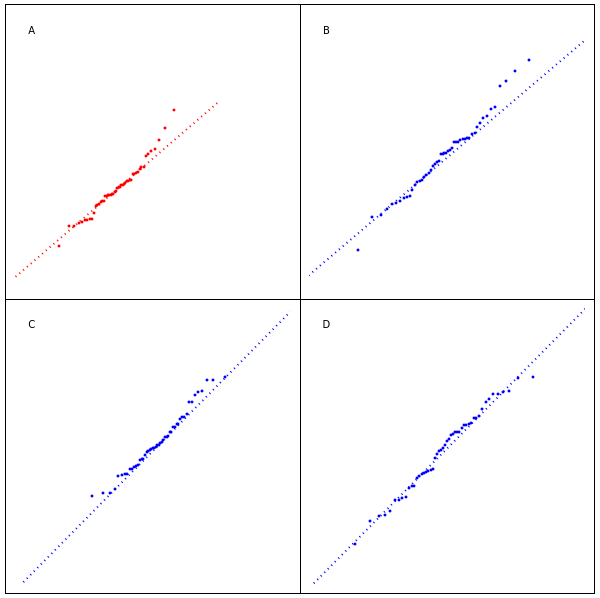
Informal Power Assessment of the Normal Probability Plot

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
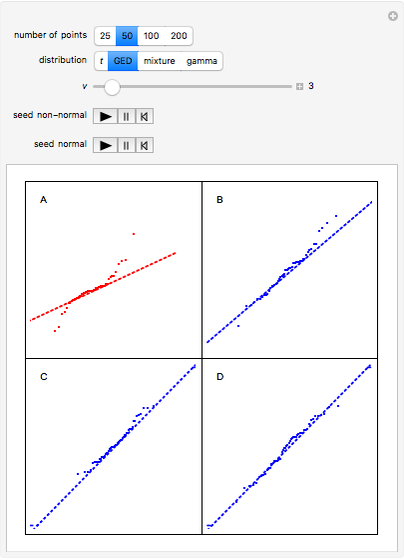
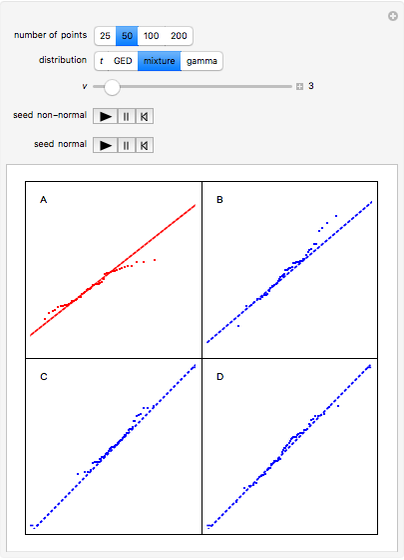
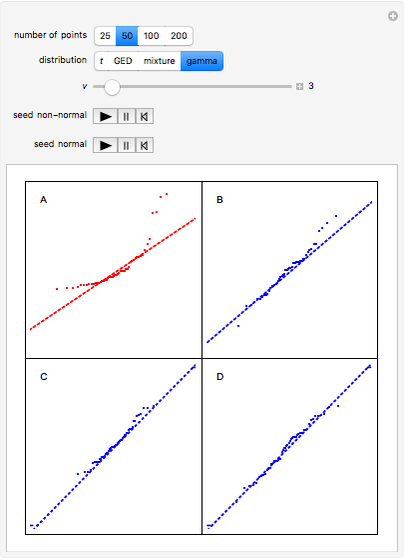
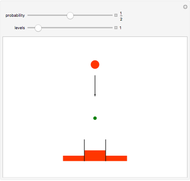
The normal probability plot or normal quantile plot for data from a variety of non-normal distributions is shown in panel A, while the other panels show the plot for normally distributed data. Since our interest is in how the data departs from the dotted straight line, the scales that would usually be shown have been suppressed to improve the visualization. By running the animation under "seed-normal", you can examine many cases in which the normal assumption holds; by comparing them with panel A, judge informally whether the features displayed in panel A are significantly non-normal. In the case of the  -distribution, as the degrees of freedom increase it becomes difficult to distinguish non-normal from normal. Larger sample sizes provide more information and help, in some cases, to make the distinction. Some other common non-normal distributions are discussed in the details.
-distribution, as the degrees of freedom increase it becomes difficult to distinguish non-normal from normal. Larger sample sizes provide more information and help, in some cases, to make the distinction. Some other common non-normal distributions are discussed in the details.
Contributed by: Ian McLeod (February 2013)
Western University
Open content licensed under CC BY-NC-SA
Snapshots
Details
The data in all plots is standardized so the mean is zero and the variance is one.
Snapshot 1: This shows the generalized error distribution (GED) or exponential distribution with shape parameter  . The Laplace and normal distributions correspond to
. The Laplace and normal distributions correspond to  respectively. When
respectively. When  , the GED has lighter-than-normal tails, while
, the GED has lighter-than-normal tails, while  corresponds to heavier tails. The GED was suggested for financial returns in [1].
corresponds to heavier tails. The GED was suggested for financial returns in [1].
Snapshot 2: This shows the contaminated normal distribution that is obtained as a mixture of two normal distributions both with mean zero; with probability 0.95 a data value is generated from the standard normal and with probability 0.05 from a normal distribution with standard deviation  . The MixtureDistribution function is used for this. The contaminated normal distribution for outliers in industrial data was suggested in [2].
. The MixtureDistribution function is used for this. The contaminated normal distribution for outliers in industrial data was suggested in [2].
Snapshot 3: This shows the gamma distribution with shape parameter,  . As
. As  increases, this distribution approximates a normal distribution.
increases, this distribution approximates a normal distribution.
References
[1] D. B. Nelson, "Conditional Heteroskedasticity in Asset Returns: A New Approach," Econometrica, 59(2), 1991, pp. 347–370. www.jstor.org/stable/2938260.
[2] J. W. Tukey, "A Survey of Sampling from Contaminated Distributions," Contributions to Probability and Statistics, (I. Olkin, ed.), Stanford, CA: Stanford University Press, 1960.
Permanent Citation