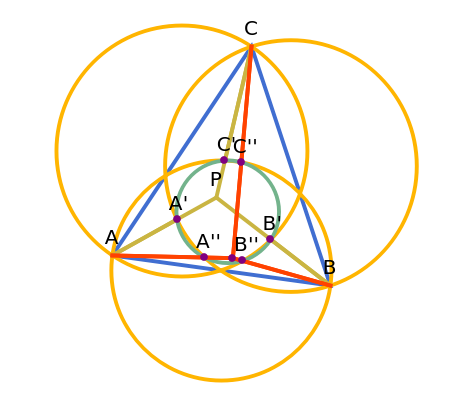Another Concurrency Generated by Circles about a Triangle's Sides and Lines through an Internal Point

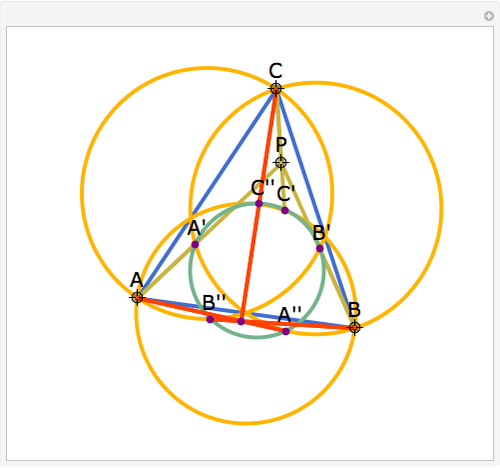
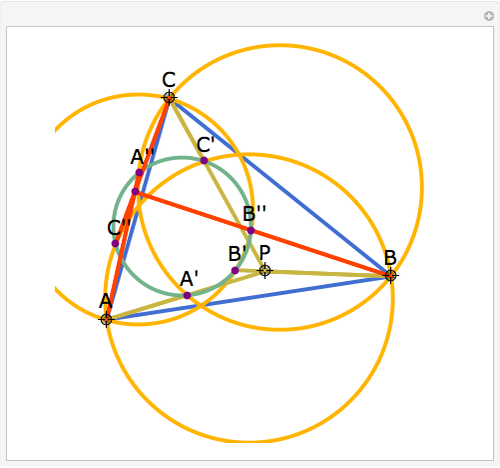
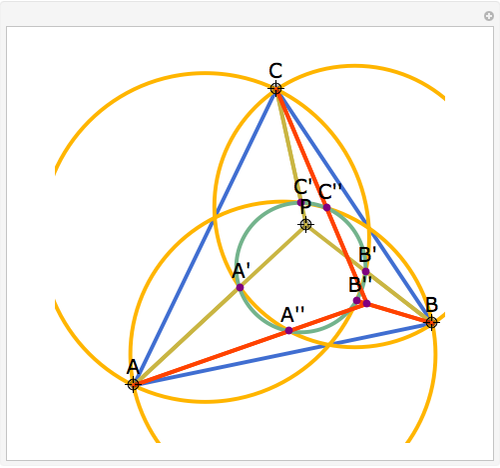
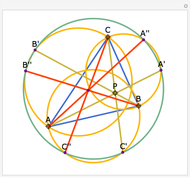
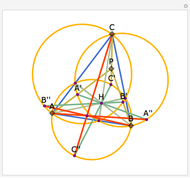
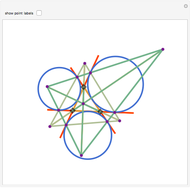
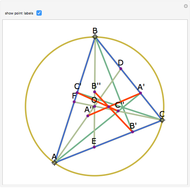
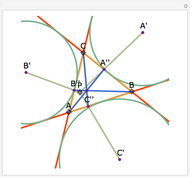
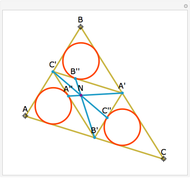
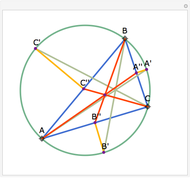
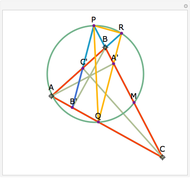
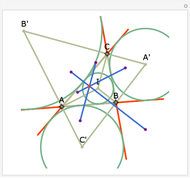
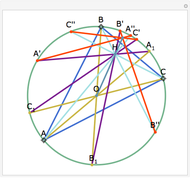
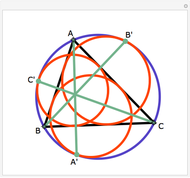
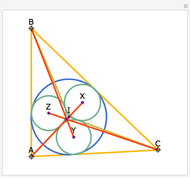
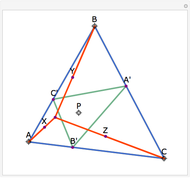
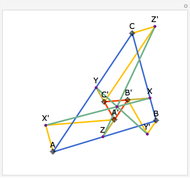
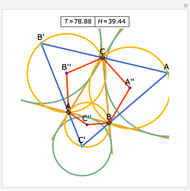
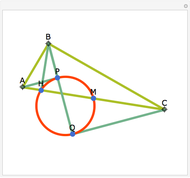
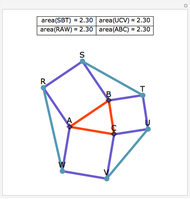
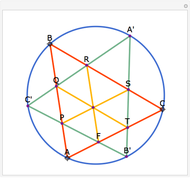
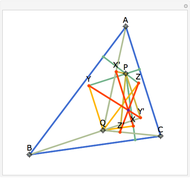
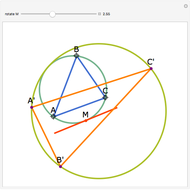
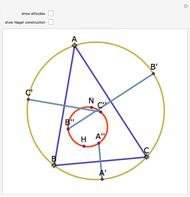
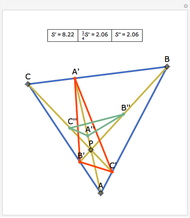
Let ABC be a triangle and P be an interior point. Let A', B', and C' be the internal intersections of AP, BP, and CP with the circles whose diameters are BC, AC, and AB, respectively. Let the circumcircle of A', B', and C' intersect the circles whose diameters are BC, AC, and AB again at A'', B'', and C''. Then AA'', BB'', and CC'' are concurrent.