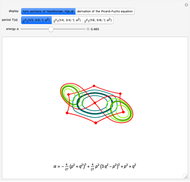
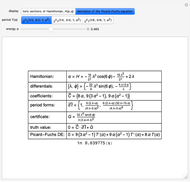
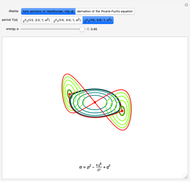
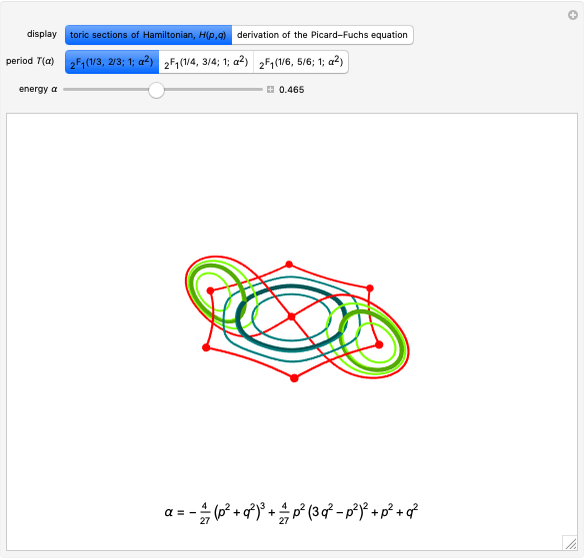
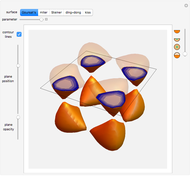
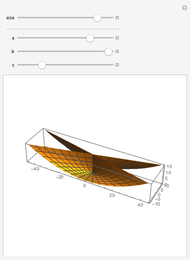
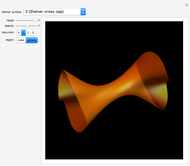
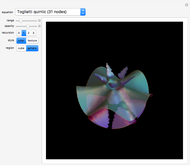
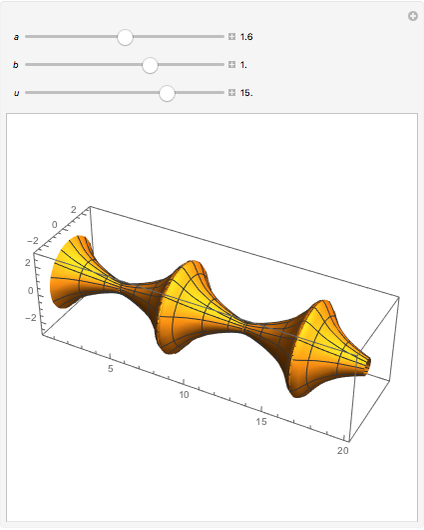
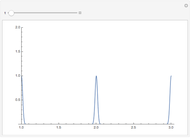
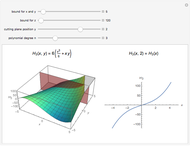
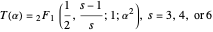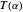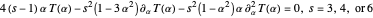A Few More Geometries after Ramanujan

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
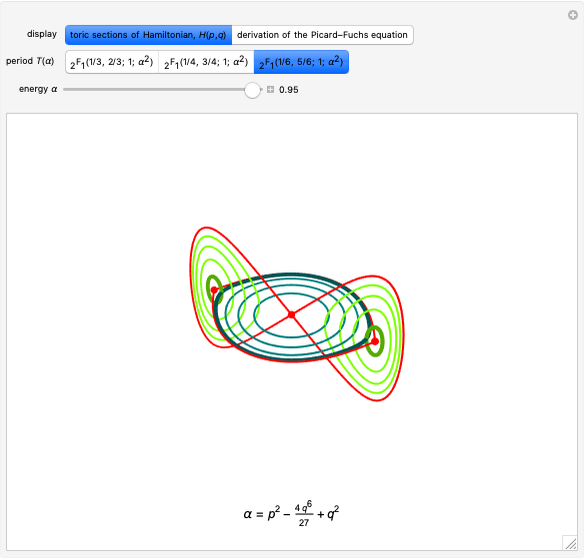
We do not know if Ramanujan had any plane curves in mind when working with the integral period functions 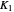 ,
, 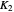 and
and 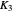 [1], though certainly these imply many simple geometries of intrinsic relevance [2]. This Demonstration gives three additional models characterized by real period functions
[1], though certainly these imply many simple geometries of intrinsic relevance [2]. This Demonstration gives three additional models characterized by real period functions
Contributed by: Brad Klee (May 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
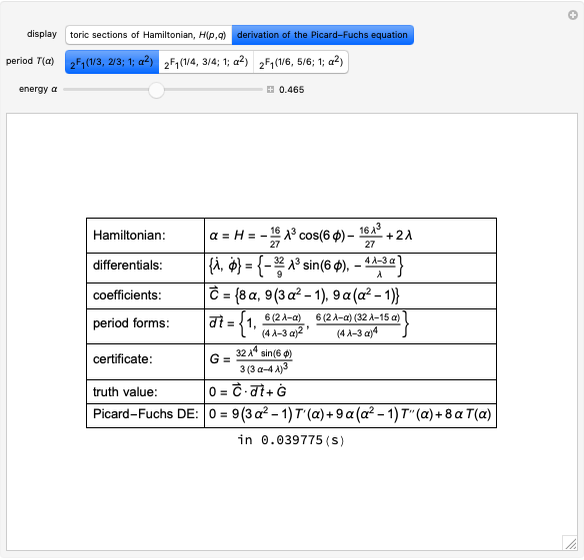
Our initial integral-differential algorithm from the Demonstration "Deriving Hypergeometric Picard–Fuchs Equations" produces results, but falls short of satisfying design goals for quality and ease of use. A subsequent Demonstration, "Approximating Pi with Trigonometric-Polynomial Integrals", gives another integral-differential algorithm that automates degree bounding and thus operates on a minimal input. The current Demonstration uses two similar functions, HEllipticPFDE[Hqp] and DihedralPFDE[Hλϕ]. Again our approach avoids general Griffiths–Dwork reduction, but otherwise follows the basic insight of [3, 4]. In this latest version, we automate degree bounding, improve variable handling and reap many new results, all with faster times.
A Hyperelliptic Case
For the more trivial function HEllipticPFDE[Hqp], inputs must have a hyperelliptic form,
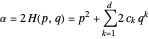
with canonical coordinates 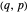 such that
such that
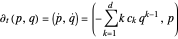 ,
,
as follows from Hamilton's equations of motion. When the potential reaches a minimum,
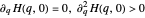 ,
,
the phase curves become loops. Each loop is measured by a period function
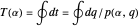 .
.
In fact, the invariant differential, 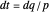 , can be integrated on any loop around the Riemannian surface
, can be integrated on any loop around the Riemannian surface 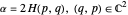 . Then we will obtain a set of period functions that satisfy an easily calculable ordinary differential equation, also called the Picard–Fuchs equation. Let vector
. Then we will obtain a set of period functions that satisfy an easily calculable ordinary differential equation, also called the Picard–Fuchs equation. Let vector 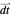 collect the one-forms,
collect the one-forms,
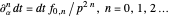 ,
,
in order of increasing 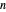 . Next assume that Hermite reduction follows a particular pattern,
. Next assume that Hermite reduction follows a particular pattern,
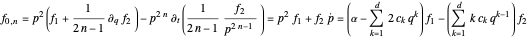 ,
,
with 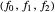 degree-bounded
degree-bounded  -polynomials. On the far right-hand side, the equation does not depend on the exponent
-polynomials. On the far right-hand side, the equation does not depend on the exponent 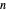 , so reduction primitives can be precomputed in matrix form. When
, so reduction primitives can be precomputed in matrix form. When
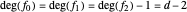 ,
,
the number of constraints equals the number of degrees of freedom equals 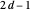 . We then solve the system of linear equations by matrix inversion. In a matrix formulation, each
. We then solve the system of linear equations by matrix inversion. In a matrix formulation, each 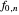 becomes a
becomes a 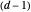 -dimensional coefficient vector subject to Hermite reduction,
-dimensional coefficient vector subject to Hermite reduction,
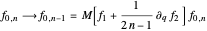 ,
,
where 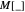 indicates encoding to a
indicates encoding to a 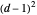 -dimensional matrix. For each element of
-dimensional matrix. For each element of 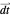 , Hermite reduction always terminates on
, Hermite reduction always terminates on 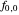 . After reducing no more than
. After reducing no more than  of the
of the 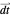 one-forms, it becomes possible to find a coefficient vector
one-forms, it becomes possible to find a coefficient vector 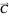 such that
such that 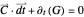 , with certificate function
, with certificate function 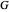 . The integral over a complete period loses the exact differential, and we then obtain the Picard–Fuchs equation,
. The integral over a complete period loses the exact differential, and we then obtain the Picard–Fuchs equation,
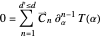 .
.
A Dihedral Case
The function DihedralPFDE[Hλϕ] operates on a more symmetrical range of plane curves. We start with a form 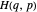 such that
such that 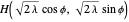 can be written in reduced terms as
can be written in reduced terms as
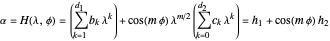 ,
,
usually with 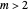 . Action angle coordinates
. Action angle coordinates 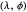 are canonical, so again by Hamilton's equations, we calculate that
are canonical, so again by Hamilton's equations, we calculate that
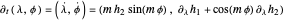 .
.
After slightly more calculus, the angle variable  may be eliminated, and we arrive at a set of three
may be eliminated, and we arrive at a set of three 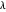 -polynomials,
-polynomials,
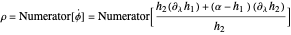 ,
,
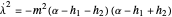 ,
,
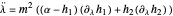 ,
,
the invariant polynomial data of 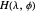 . A vector
. A vector 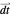 collects one-forms,
collects one-forms,
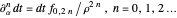 ,
,
and again we can write a pattern for all subsequent iterations of Hermite reduction,
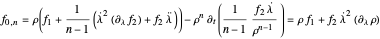 .
.
If we introduce degrees
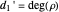
and
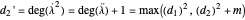 ,
,
then we must also require that
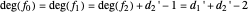 .
.
This is the unique degree-bounding constraint where Hermite reduction becomes operable as
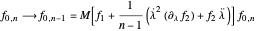 ,
,
again with matrix encoding  . For each element of
. For each element of 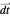 , care must be taken in case the initial numerator satisfies
, care must be taken in case the initial numerator satisfies
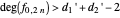 .
.
If so, we must precede Hermite reduction by expansion in partial fractions. Then recursive calculations always terminate on 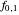 . After reducing no more than
. After reducing no more than 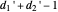 of the
of the 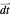 one-forms, it again becomes possible to find a coefficient vector
one-forms, it again becomes possible to find a coefficient vector 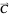 such that
such that
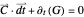 ,
,
with certificate function 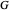 . Again, the Picard–Fuchs equation,
. Again, the Picard–Fuchs equation,
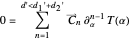 ,
,
follows immediately.
Certificates and Complexity
Both algorithms HEllipticPFDE[Hqp] and DihedralPFDE[Hλϕ] sow enough information to check coefficient vector 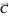 against certificate function
against certificate function 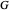 after evaluation. A successful computation is easy to validate by evaluating the expression
after evaluation. A successful computation is easy to validate by evaluating the expression 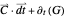 , hopefully to a truth value 0, as is done in this Demonstration. It should be clear from the preceding discussion that computation of
, hopefully to a truth value 0, as is done in this Demonstration. It should be clear from the preceding discussion that computation of 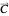 does not depend on computation of
does not depend on computation of 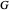 . However, components of
. However, components of 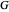 are also computed by matrix multiplication in a relatively short time. Thus we are able to print and check the certificate functions without too much extra work.
are also computed by matrix multiplication in a relatively short time. Thus we are able to print and check the certificate functions without too much extra work.
How much work are we actually doing? And are we doing too much? If  is the dimension of the
is the dimension of the 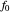 vector space, then matrix inversion, matrix-encoded Hermite reduction and finding the nullspace all have an arithmetic complexity estimated roughly as
vector space, then matrix inversion, matrix-encoded Hermite reduction and finding the nullspace all have an arithmetic complexity estimated roughly as 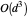 . If partial decomposition becomes necessary, the dihedral algorithm can potentially slow to
. If partial decomposition becomes necessary, the dihedral algorithm can potentially slow to 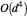 . Both polynomial figures are quite minimal, and compare well to complexity figures for other algorithms designed specifically for bivariate polynomials [4]. In practice, arithmetic complexity is somewhat misleading, and it is easy to notice exponential slowdown, especially when the size of the output coefficients and certificates begins to become unmanageably large.
. Both polynomial figures are quite minimal, and compare well to complexity figures for other algorithms designed specifically for bivariate polynomials [4]. In practice, arithmetic complexity is somewhat misleading, and it is easy to notice exponential slowdown, especially when the size of the output coefficients and certificates begins to become unmanageably large.
More and More Interesting Geometry!
The new functions allow us to repeat and improve upon earlier calculations of "Deriving Hypergeometric Picard-Fuchs Equations", where elliptic Hamiltonians were measured by another special case of the hypergeometric differential equation
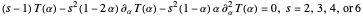 .
.
With the present Demonstration, we extend the range of geometries by three more interesting specimens featuring dihedral symmetry. Although we avoid Griffiths–Dwork reduction, the algorithms HEllipticPFDE[Hqp] and DihedralPFDE[Hλϕ] are not overly simple. They can produce many more interesting certificates!
The code commented out in the section Initialization Code contains numerous examples, but let us mention the Euler periods in particular. In a somewhat surprising success of input hacking, the function DihedralPFDE[Hλϕ] also enables analysis of periods of algebraic sphere curves. In fact, an earlier prototype of DihedralPFDE[Hλϕ] was used for the author's original derivation of differential equations associated to Goursat surfaces (cf. [5–7]). Quite amazingly, the real Euler period of the tetrahedral-symmetric, cubic sphere curves yet again takes a hypergeometric form,
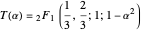 .
.
References
[1] S. Ramanujan, "Modular Equations and Approximations to 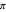 ," Quarterly Journal of Mathematics, 45, 1914 pp. 350–372. ramanujan.sirinudi.org/Volumes/published/ram06.pdf.
," Quarterly Journal of Mathematics, 45, 1914 pp. 350–372. ramanujan.sirinudi.org/Volumes/published/ram06.pdf.
[2] L. C. Shen, "On Three Differential Equations Associated with Chebyshev Polynomials of Degrees 3, 4 and 6," Acta Mathematica Sinica, 33(1), 2017 pp. 21–36. doi:10.1007/s10114-016-6180-1.
[3] P. Lairez, "Computing Periods of Rational Integrals," Mathematics of Computation, 85, 2016 pp. 1719–1752. doi:10.1090/mcom/3054.
[4] A. Bostan, S. Chen, F. Chyzak and Z. Li, "Complexity of Creative Telescoping for Bivariate Rational Functions." arxiv.org/abs/1301.5045.
[5] N. J. A. Sloane and B. Klee. The On-Line Encyclopedia of Integer Sequences. oeis.org/A006480.
[6] B. Klee. The On-Line Encyclopedia of Integer Sequences. oeis.org/A318245.
[7] B. Klee. The On-Line Encyclopedia of Integer Sequences. oeis.org/A318495.
Permanent Citation