A New Kind of Casimir Energy and Its Implications for Dark Energy

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
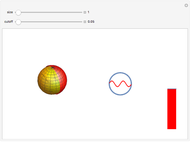
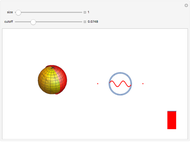
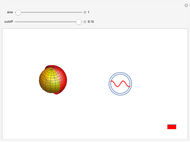
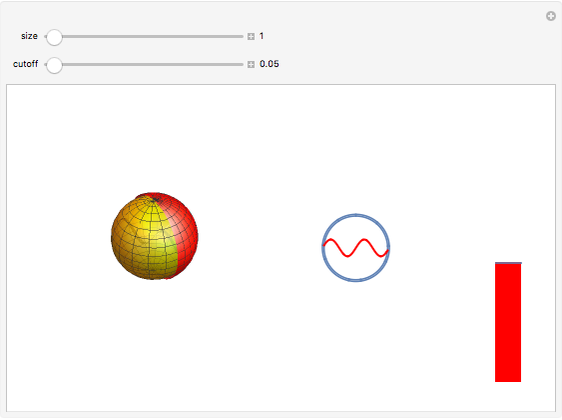
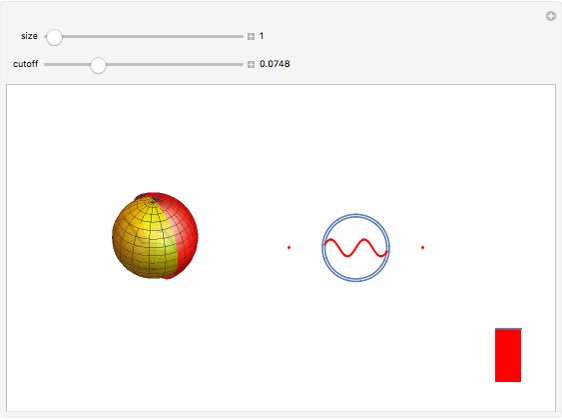
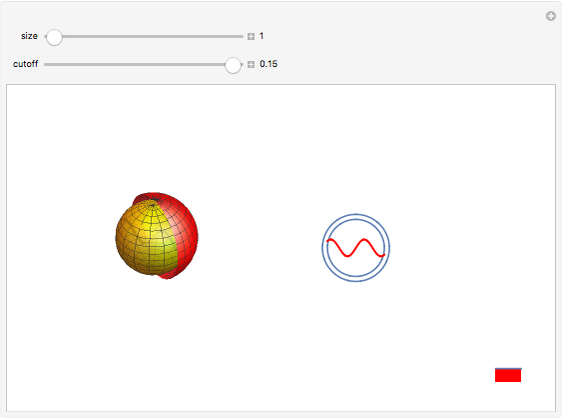
We propose to use metamaterials to mimic de Sitter space. This Demonstration represents the behavior of Casimir energy in a cavity with size  and physical cut-off
and physical cut-off  . In this case the total Casimir energy is proportional to
. In this case the total Casimir energy is proportional to  . Notably, this would play a role of dark energy and give a possible explanation of cosmic acceleration if
. Notably, this would play a role of dark energy and give a possible explanation of cosmic acceleration if  is identified with the Plank scale. This result can be tested experimentally.
is identified with the Plank scale. This result can be tested experimentally.
Contributed by: Miao Li,Xiaodong Li, and Yi Pang (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
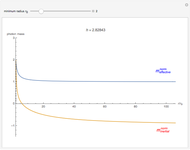
The existence of Casimir energy is one of the important predictions in quantum field theory and continues to be a source of inspiration for theoretical as well as experimental work [1]. Generically, the expression of the Casimir energy depends on details of the cavity including properties of its bulk and boundary. The earliest work on Casimir energy and the follow-up studies [3] all reported that the Casimir energy density is inversely proportional to the fourth power of the typical size of the cavity. Applying this result to the universe, this kind of Casimir energy cannot be taken as a possible origin of dark energy, since  is too small compared with the observed dark energy density [4] if
is too small compared with the observed dark energy density [4] if  is chosen to be the estimated size of the universe.
is chosen to be the estimated size of the universe.
With doubt about the applicability of the previous results to de Sitter space, we carried out a careful calculation of the Casimir energy density of the electromagnetic field in the static patch of de Sitter space [5]. A drastically different Casimir energy was obtained that is proportional to the size of the event horizon taking the same form as holographic dark energy [6]. Then based on recent theoretical and experimental developments in metamaterials [7], [8], we proposed the design of metamaterials mimicking de Sitter space. Specifically, the permittivity and permeability are given by the following expressions:  , where
, where  ,
,  represent the Cartesian coordinates,
represent the Cartesian coordinates,  is the radial distance, and
is the radial distance, and  is the boundary of the cavity. These differ from the usual expressions for the permittivity and permeability parameters in that they have divergent components tangent to the boundary. This fact leads to a brand new type of Casimir energy in the cavity coinciding with the result from gravitational theory with the Planck scale replaced by some microscopic scale (denoted by
is the boundary of the cavity. These differ from the usual expressions for the permittivity and permeability parameters in that they have divergent components tangent to the boundary. This fact leads to a brand new type of Casimir energy in the cavity coinciding with the result from gravitational theory with the Planck scale replaced by some microscopic scale (denoted by  ) in metamaterials. We encourage experimentalists to make such metamaterials and measure the predicted Casimir energy. This work would have significant implications in cosmology.
) in metamaterials. We encourage experimentalists to make such metamaterials and measure the predicted Casimir energy. This work would have significant implications in cosmology.
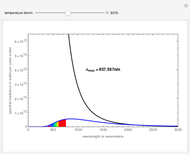
It is probably difficult to carry out such an experiment because the Casimir energy consists of a sum over all frequencies, so that each frequency makes a contribution. By contrast, metamaterials have frequency dispersion, so that the designed permittivity and permeability are effective only to frequencies in a finite band. However, this difficulty can be circumvented because there is a typical frequency whose contribution to the Casimir energy is dominant [9]. According to our estimate, the typical dominating frequency is of the order of  with the dominant angular quantum number
with the dominant angular quantum number  ∼
∼ . Thus a cavity of metamaterials effective at this typical frequency can mimic de Sitter space and induces the Casimir energy predicted by the theoretical calculation. These two numbers give the same leading term in Casimir energy,
. Thus a cavity of metamaterials effective at this typical frequency can mimic de Sitter space and induces the Casimir energy predicted by the theoretical calculation. These two numbers give the same leading term in Casimir energy,  , as in our previous result [5]. Thus a cavity of metamaterials effective at this typical frequency can mimic de Sitter space and induce a Casimir energy predicted by theoretical calculation.
, as in our previous result [5]. Thus a cavity of metamaterials effective at this typical frequency can mimic de Sitter space and induce a Casimir energy predicted by theoretical calculation.
We hope that one day the metamaterials with the properties we suggest can be made so that the predicted new type of Casimir energy can be measured, thus providing a laboratory analog for cosmology.
References:
[1] M. Bordag, ed., The Casimir Effect 50 Years Later, Hackensack, NJ: World Scientific, 1999.
[2] H. B. G. Casimir, "On the Attraction between Two Perfectly Conducting Plates," Proceedings of the American Philosophical Society, 51, 1948 pp. 793–795.
[3a] T. H. Boyer, "Quantum Electromagnetic Zero-Point Energy of a Conducting Spherical Shell and the Casimir Model for a Charged Particle," Phys. Rev., 174, 1968 p. 1764.
[3b] R. Balian and B. Duplantier, "Electromagnetic Waves Near Perfect Conductors. 2. Casimir Effect," Annals Phys., 112, 1978 p. 165.
[3c] K. A. Milton, L. L. De-Raad, and J. S. Schwinger, "Casimir Self-Stress on a Perfectly Conducting Spherical Shell," Ann. Phys., 115, 1978 pp. 288–403.
[4a] A. G. Riess, et al., "Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant," Astron. J., 116, 1998 p. 1009.
[4b] S. Perlmuttter, et al., The Astrophysical Journal, 517(2), 1999 p. 565.
[5] M. Li, R. X. Miao, and Y. Pang, "Casimir Energy, Holographic Dark Energy and Electromagnetic Metamaterial Mimicking de Sitter," arXiv, 2009.
[6] M. Li, "A Model of Holographic Dark Energy," Phys. Lett. B, 603(1–2), 2004 p. 1.
[7a] J. Plebanski, "Electromagnetic Waves in Gravitational Fields," Phys. Rev., 118, 1959 p. 1396.
[7b] U. Leonhardt, "Optical Conformal Mapping," Science, 312, 2006 p. 1777.
[7c] J. B. Pendry, D. Schurig, and D. R. Smith, "Controlling Electromagnetic Fields," Science, 312, 2006 p. 1780.
[8a] R. A. Shelby, D. R. Smith, and S. Shultz, "Experimental Verification of a Negative Index of Refraction," Science, 292, 2001 p. 77.
[8b] E. Cubukcu, K. Aydin, E. Ozbay, S. Foteinopoulou, and C. M. Soukoulis, "Electromagnetic Waves: Negative Refraction by Photonic Crystal," Nature, 423, 2003 p. 604.
[8c] D. R. Smith, J. B. Pendry, and M. C. K. Wiltshire, "Metamaterials and Negative Refractive Index," Science, 305, 2004 p. 788.
[8d] D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr, and D. R. Smith, "Metamaterials Electromagnetic Cloak at Microwave Frequencies," Science, 314, 2006 p. 977.
[9] M. Li, R. X. Miao, and Y. Pang, "More Studies on Metamaterials Mimicking de Sitter," arXiv, 2009.
Permanent Citation