The Casimir Effect

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
According to quantum electrodynamics, the vacuum, even in the absence of photons, is filled with zero-point energy (ZPE) from all modes  of the electromagnetic field, given by
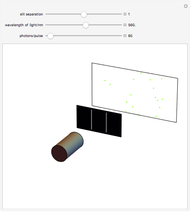
of the electromagnetic field, given by  . The ZPE of the vacuum is infinite unless regularized by frequency cutoffs or other stratagems. In most electromagnetic phenomena, the ZPE can be canceled out or renormalized away. Casimir and Polder in 1948 proposed a physical situation in which the effects of ZPE might be directly observable. They considered two perfectly conducting parallel plates, with area
. The ZPE of the vacuum is infinite unless regularized by frequency cutoffs or other stratagems. In most electromagnetic phenomena, the ZPE can be canceled out or renormalized away. Casimir and Polder in 1948 proposed a physical situation in which the effects of ZPE might be directly observable. They considered two perfectly conducting parallel plates, with area  , separated by a distance
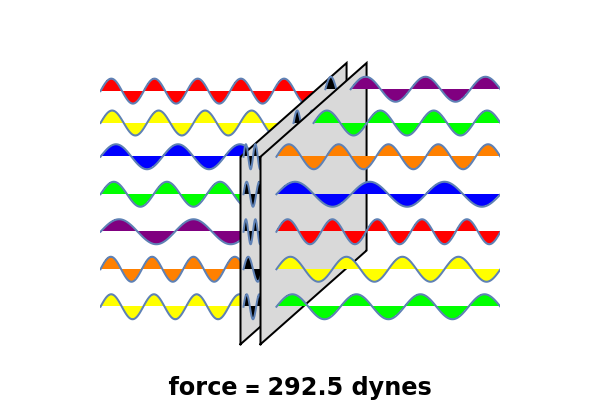
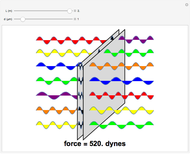
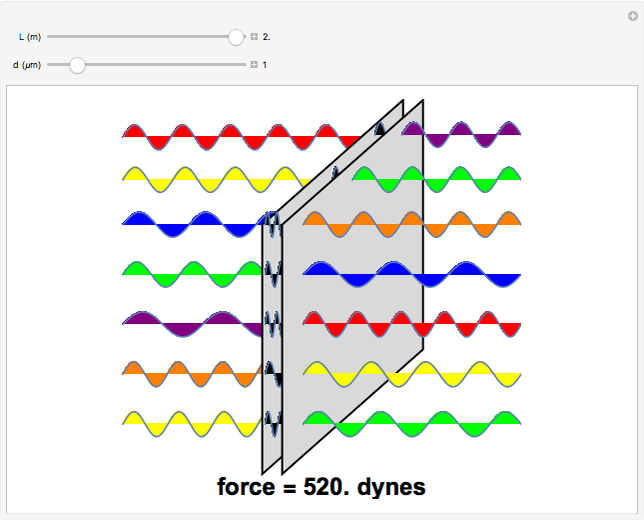
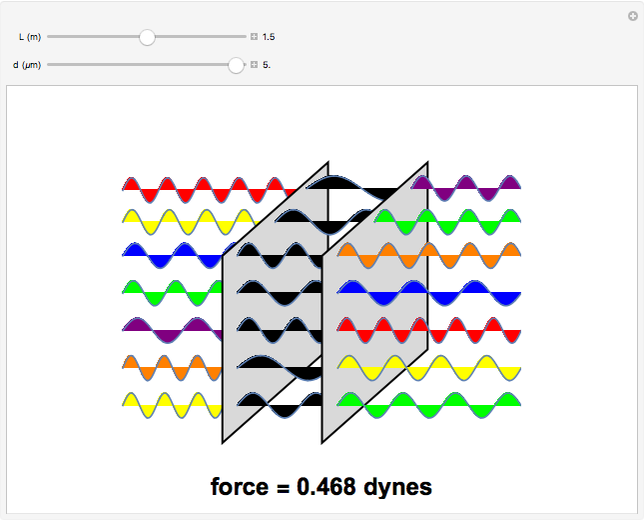
, separated by a distance  of the order of microns. The electric field inside a perfect conductor equals zero, so this gives boundary values of zero for all modes at the surface. This perturbs the zero-point modes of the electromagnetic field, since modes with horizontal wavelength components greater than
of the order of microns. The electric field inside a perfect conductor equals zero, so this gives boundary values of zero for all modes at the surface. This perturbs the zero-point modes of the electromagnetic field, since modes with horizontal wavelength components greater than  will be excluded from the region between the plates. They will lie in the ultraviolet and beyond and are shown as black waves. Modes outside the plates can belong to a continuum of frequencies. The result is a net attractive force -
will be excluded from the region between the plates. They will lie in the ultraviolet and beyond and are shown as black waves. Modes outside the plates can belong to a continuum of frequencies. The result is a net attractive force - . In the above formulas
. In the above formulas  is the reduced Planck's constant (
is the reduced Planck's constant ( ),
),  is the speed of light and
is the speed of light and  is the frequency of the mode
is the frequency of the mode  . Note that this force is a purely quantum effect since it vanishes for
. Note that this force is a purely quantum effect since it vanishes for  . It is also independent of the electric charge
. It is also independent of the electric charge  . Measurement of the Casimir–Polder force involves very delicate experiments, but its validity has been successfully verified to better than 1% accuracy.
. Measurement of the Casimir–Polder force involves very delicate experiments, but its validity has been successfully verified to better than 1% accuracy.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Casimir effect: Wikipedia article
Permanent Citation