The Zeeman Effect in the Interstellar Medium

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
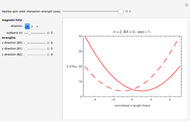
This Demonstration discusses the effects of a magnetic field on observations of certain emission lines. Strong magnetic fields can split emission and absorption lines, an effect discovered by Pieter Zeeman in 1896. This is one of the very few ways scientists can measure magnetic field strength in the interstellar medium. By matching the observed Stokes V profile with a scaled derivative of the Stokes I (details below), the line-of-sight strength of the magnetic field can be determined.
Contributed by: Lauren Woolsey (May 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A spectral line is produced in an atomic or molecular transition from one state to another, usually when an electron changes energy levels. However, for neutral hydrogen at 21 cm and for the OH lines at 1665 and 1667 MHz, the lines originate from the electron spin flip from parallel to the spin of the nucleus to antiparallel. When a magnetic field is introduced into the region, the frequency of this emission line can be shifted. The amount of this shift is proportional to a Zeeman splitting factor ( ) and the strength of the magnetic field,
) and the strength of the magnetic field,
 .
.
The resolution of this measurement is proportional to  , so to detect this effect, which is often very small, astronomers focus on spectral lines at radio wavelengths, where
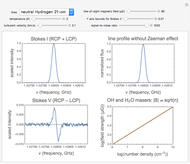
, so to detect this effect, which is often very small, astronomers focus on spectral lines at radio wavelengths, where  is small enough for the resolution of the telescopes used. If the effect is large enough, the lines split fully into two parts that can be measured separately by the total intensity or the Stokes I parameter. The Stokes I parameter shows the sum of right circularly polarized (RCP) light and left circularly polarized (LCP) light. However, if the effect is small, the line does not change significantly. To measure the magnetic field, we must then look at the Stokes V parameter, which is the difference between RCP and LCP intensity. The Stokes V intensity can be fit using a derivative of the Stokes I intensity scaled up by the magnetic field strength,
is small enough for the resolution of the telescopes used. If the effect is large enough, the lines split fully into two parts that can be measured separately by the total intensity or the Stokes I parameter. The Stokes I parameter shows the sum of right circularly polarized (RCP) light and left circularly polarized (LCP) light. However, if the effect is small, the line does not change significantly. To measure the magnetic field, we must then look at the Stokes V parameter, which is the difference between RCP and LCP intensity. The Stokes V intensity can be fit using a derivative of the Stokes I intensity scaled up by the magnetic field strength,
 .
.
This effect can only measure the intensity of the magnetic field along the line of sight,  . Other methods of measuring magnetic fields in the interstellar medium make use of Faraday rotation and polarization of starlight or dust emission. The Zeeman effect is one of the best measures of magnetic field, but it can only be used in dense regions with strong magnetic fields like molecular clouds.
. Other methods of measuring magnetic fields in the interstellar medium make use of Faraday rotation and polarization of starlight or dust emission. The Zeeman effect is one of the best measures of magnetic field, but it can only be used in dense regions with strong magnetic fields like molecular clouds.
References:
[1] R. M. Crutcher, "Magnetic Fields in Molecular Clouds: Observations Confront Theory," The Astrophysical Journal, 520(2), 1991 pp. 706–713. doi:10.1086/307483.
[2] A. A. Goodman, R. M. Crutcher, C. Heiles, P. C. Myers, and T. H. Troland, "Measurement of Magnetic Field Strength in the Dark Cloud Barnard 1," The Astrophysical Journal: Letters, 338, 1989 pp. L61–L64. doi:10.1086/185401.
[3] J-L. Han, R. Wielebinski, "Milestones in the Observations of Cosmic Magnetic Fields," Chinese Journal of Astronomy and Astrophysics, 2(4), 2002 pp. 293–324. doi:10.1088/1009-9271/2/4/293.
[4] C. Heiles, A. A. Goodman, C. F. McKee, and E. G. Zweibel, "Magnetic Fields in Star-Forming Regions: Observations," in Protostars and Planets III (E. H. Levy and J. I. Lunine, eds.), Tuscon: University of Arizona Press, 1993.
[5] C. F. McKee, E. G. Zweibel, A. A. Goodman, and C. Heiles, "Magnetic Fields in Star-Forming Regions: Theory," in Protostars and Planets III (E. H. Levy and J. I. Lunine, eds.), Tuscon: University of Arizona Press, 1993.
[6] G. B. Rybicki and A. P. Lightman, Radiative Processes in Astrophysics, Weinheim, Germany: Wiley-VCH, 2004.
[7] A. P. Sarma, C. L. Brogan, T. L. Bourke, M. Eftimova, and T. H. Troland, "Very Large Array OH Zeeman Observations of the Star-Forming Region S88B," The Astrophysical Journal, 767(1), 2013 p. 24. doi:10.1088/0004-637X/767/1/24.
Permanent Citation