Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Triangle Formed by the Centers of Three Nine-Point Circles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

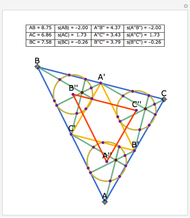
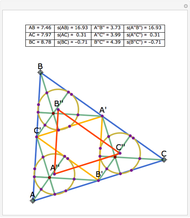
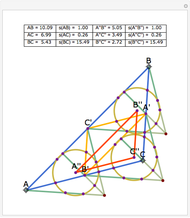
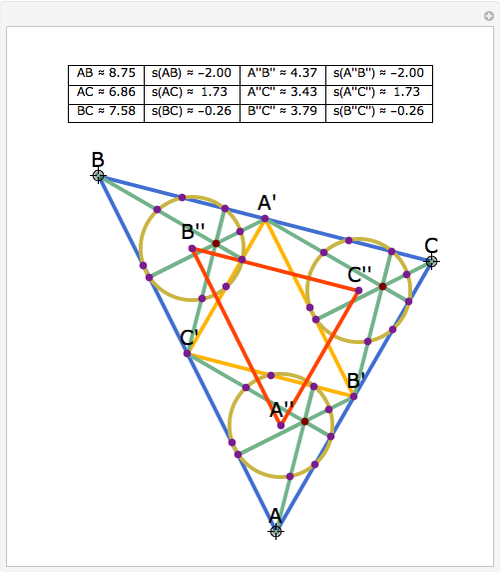
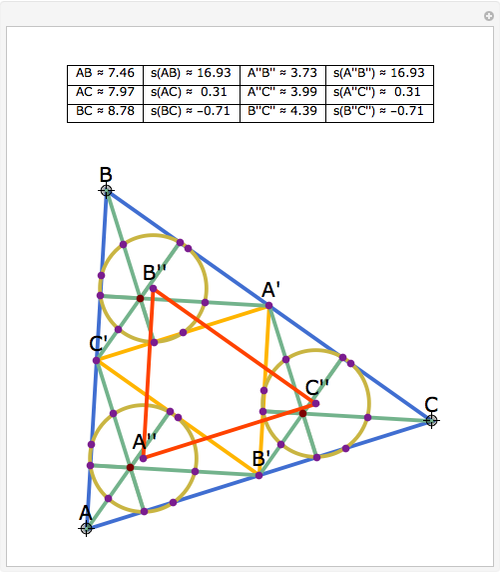
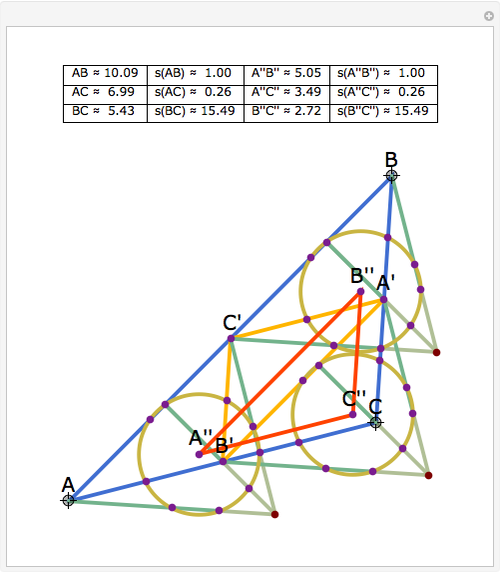
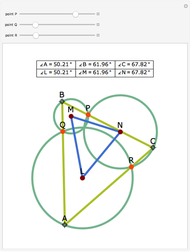
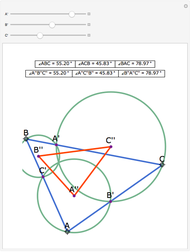
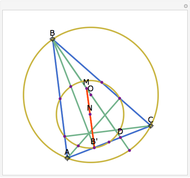
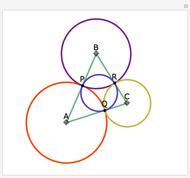
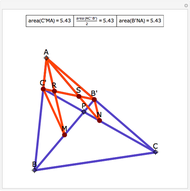
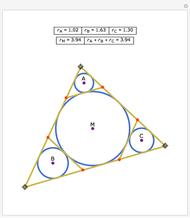
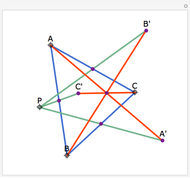
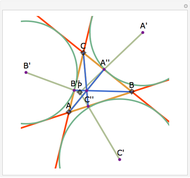
Let ABC be a triangle and let A', B', and C' be the midpoints of BC, AC, and AB, respectively. Let A'', B'', and C'' be the centers of the nine-point circles of the triangles AB'C', BC'A', and CA'B', respectively. Then A''B''C'' is homothetic with ABC in the ratio 1:2.

[more]

In the figure s(XY) is the slope of XY.

[less]

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

See problem 72 in N. Altshiller-Court, College Geometry, 2nd ed., Mineola, NY: Dover, 2007 p. 120.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send