The Center and Radius of the Nine-Point Circle

Initializing live version

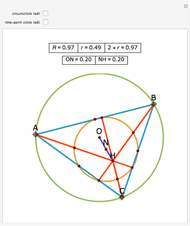
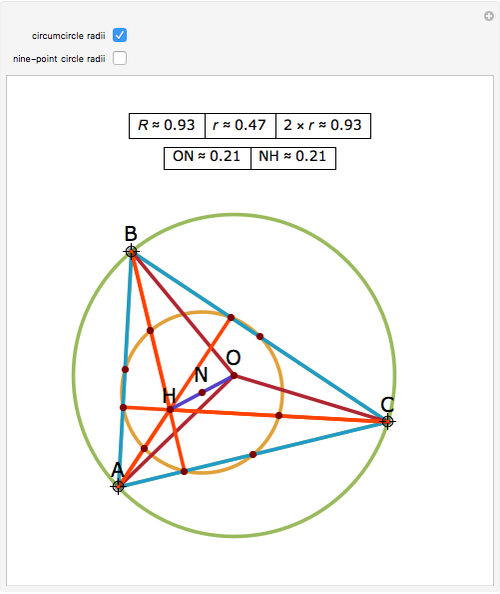
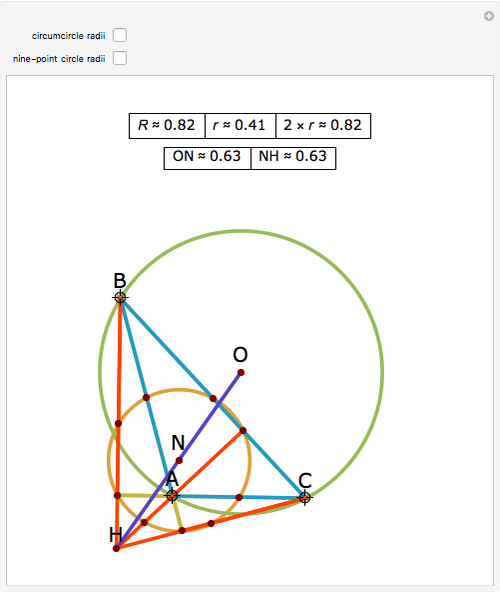
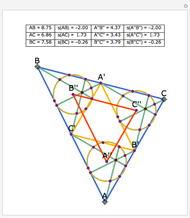
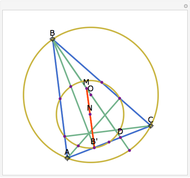
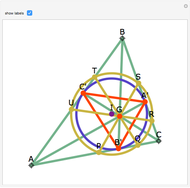
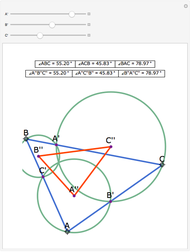
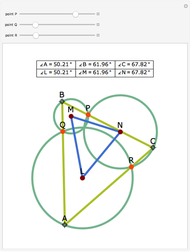
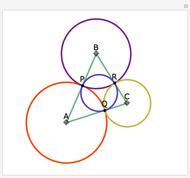
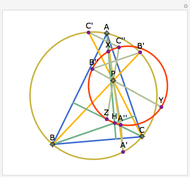
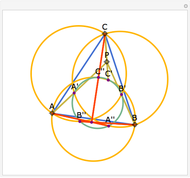
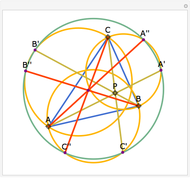
Let ABC be a triangle with orthocenter H, circumcenter O, and circumradius 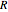. Let the nine-point circle have center N and radius .

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

See theorem 209 in N. Altshiller-Court, College Geometry, Mineola, NY: Dover, 2007 p. 104.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send