Adams' Circle and the Gergonne Point

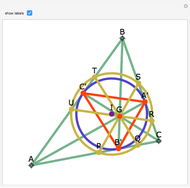
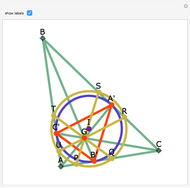
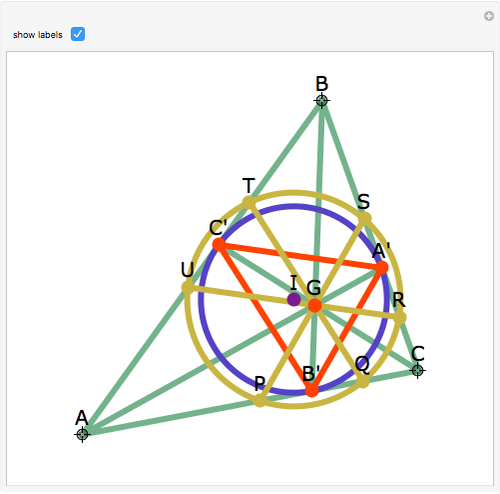
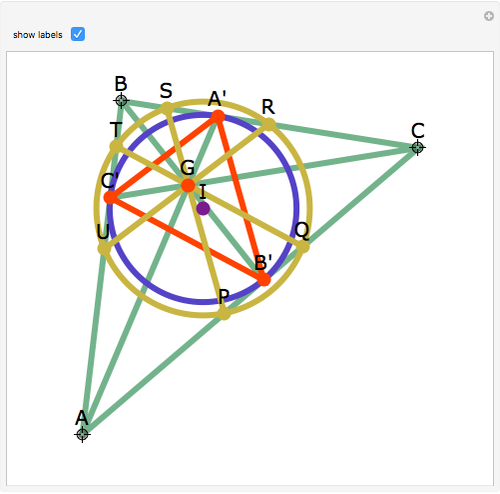
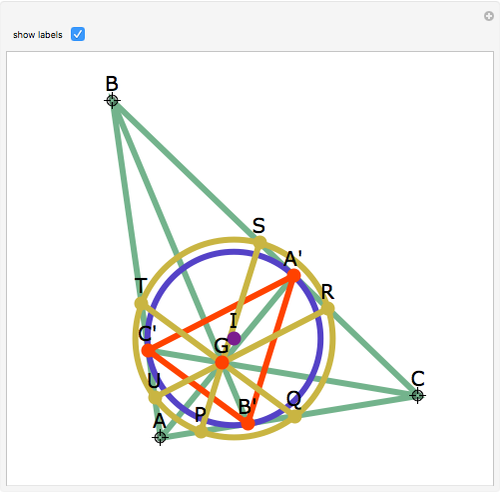
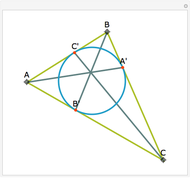
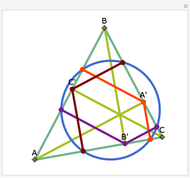
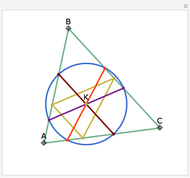
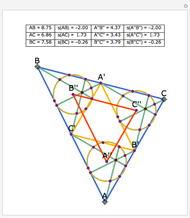
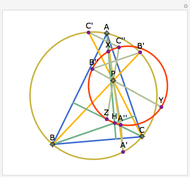
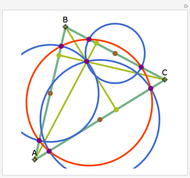
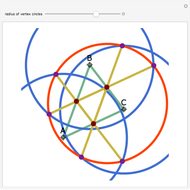
Let ABC be a triangle and let A'B'C' be the contact triangle, whose vertices are the points where the incircle intersects ABC. The lines AA', BB' and CC' meet at the point G, called the Gergonne point. Draw lines through G and parallel to the sides of the contact triangle. These lines meet the sides of ABC in six concyclic points: P, Q, R, S, T, and U; that circle is called the Adams circle of ABC. Also, the incenter I of ABC is the center of the Adams circle.